9. クエリ効率の良いプランニングの限界

前回の講義を復習してみよう。あるMDP $M = (\mathcal{S},\mathcal{A},P,r,\gamma)$にシミュレータで$M$とインタラクションした時を考える。このとき、特徴マップ $\varphi: \mathcal{S}\times\mathcal{A}\to \mathbb{R}^d$、事前に計算したsuitably small core set(Kiefer-Wolfowitzh定理の$\mathcal{C}$のこと？)、$\varepsilon’>0$なるターゲット、信頼パラメータ$0\le \zeta \le 1$について、最大で$\text{poly}(\frac{1}{1-\gamma},d,\mathrm{A},\frac{1}{(\varepsilon’)^2},\log(1/\zeta))$の計算時間でLSPIは重みベクトル$\theta\in \mathbb{R}^d$を返す。この重みベクトルは、$q = \Phi \theta$について貪欲な方策は確率$1-\zeta$で次の$\delta$について$\delta$-最適になる:

\[\begin{align} \delta \le \frac{2(1 + \sqrt{d})}{(1-\gamma)^2}\, \varepsilon + \varepsilon'\,, \label{eq:suboptapi} \end{align}\]

ここで$\varepsilon$は、MDPについて、方策の行動価値関数を近似したときの誤差である:

\[\begin{align} \varepsilon = \varepsilon^*(M,\Phi) : = \sup_{\pi \text{ memoryless}} \inf_{\theta\in \mathbb{R}^d} \| \Phi \theta - q^\pi \|_\infty\,. \label{eq:polerr} \end{align}\]

前回までの講義に則り、$\Phi$は全状態行動対についての特徴ベクトル$\varphi^\top(s,a)$を固定された順番で組み合わせて得られる$| \mathcal{S}\times\mathcal{A} | \times d$の行列である。 $\varepsilon’$ を式. \eqref{eq:suboptapi}の最初の項に合わせれば、$1/\varepsilon$を含んだ?多項式の計算時間に収まる。しかし、無限時間計算したとしても、取り得る最良のバウンドは

\[\begin{align} \delta \le \frac{2(1 + \sqrt{d})}{(1-\gamma)^2}\, \varepsilon\,. \label{eq:limit} \end{align}\]

である。

妥当な計算量であれば、$\delta$が$\varepsilon$および$\varepsilon$の定数倍よりも優れていることはありえないということは理解できるが、余分な$\sqrt{d}/(1-\gamma)^3$が本当に必要であるかどうかは不明である。おそらく$1/(1-\gamma)$にまつわる項が必要であることは理解できるだろう。なぜなら、$q^*$について最良の近似を与えるパラメータベクトルがあるとしても、$q^*$について貪欲に行動したときの誤差は

\[\frac{\varepsilon}{1-\gamma}\,\]

になるためだ。

しかし、この時点では、余分な $\sqrt{d}$ が必要かどうかは全く不明だ。今回の講義では、「この余分な$\sqrt{d}$にまつわる要素は本当に必要なのか？」を議論していく。もしくは、より小さな準最適性を持つ方策を生成することができる他の多項式実行時間アルゴリズムが存在するのだろうか？

この講義では、この疑問に対して部分的に答えを示す。つまり、$\sqrt{d}$が必要であることを示していく。まず、行動の数に制限がない場合、効率的なアルゴリズムは$\delta = \Omega( \varepsilon\sqrt{d})$に制限されることを示す下界から始める。

行動空間が大きいMDPのクエリの下界

まず、以下の便利な定義から始める。

定義 (soundness): ローカルプランナーが次の条件を満たす場合、$(\delta,\varepsilon)$-soundである: 任意の有限割引MDP $M=(\mathcal{S},\mathcal{A},P,r,\gamma)$と$\varepsilon^*(M,\Phi)\le \varepsilon$なる特徴マップ $\varphi:\mathcal{S}\times \mathcal{A}\to \mathbb{R}^d$に対し、プランナーが$(M,\varphi)$とインタラクションし、$\delta$-最適な方策に至る。

定義 (メモリーレスプランナー): 呼び出しごとに何の情報も保持しないプランナーは メモリーレス である。

これから示していく下界を次に示す:

Theorem (クエリの下界: 行動空間が大きい場合): 任意の$\varepsilon>0$, $0<\delta\le 1/2$, 正の整数$d$と、任意の$(\delta,\varepsilon)$-soundなローカルプランナー$\mathcal{P}$について、報酬が$[0,1]$であり、次を満たす”featurized-MDP” $(M,\varphi)$が存在する: $(M,\varphi)$のシミュレータとインタラクションした時、$\mathcal{P}$の利用に期待されるクエリの数は最低でも

\[\begin{align*} \Omega\left( \exp\left( \frac{1}{32} \left(\frac{\sqrt{d}\varepsilon}{\delta}\right)^2 \right) \right)\,. \end{align*}\]

である。

ここで、$\delta=\varepsilon$ もしくはそれより小さい場合、クエリの数は$d$について指数的になることに注意して欲しい。この証明には「$d$次元の単位球に、ほぼ直交する$d$について指数個のベクトルを詰め込むことができる」ことを示す結果が必要である。正確な結果は、証明なしで述べるが、次のようになる:

Lemma (Johnson-Lindenstrauss (JL) の補題) 次を満たす全ての$\tau > 0$ と整数$d,k$を考える。

\[\left\lceil\frac{8 \ln k}{\tau^2}\right\rceil \leq d \leq k\]

この時、全ての$1\le i<j\le k$について、次を満たす$d$次元の単位球のベクトル$v_1,…,v_k$が存在する。

\[\lvert \langle v_i,v_j \rangle | \leq \tau\,.\]

ここで、固定された次元$d$について、妥当な$k$の範囲は

$\begin{align} d\le k \le \exp\left(\frac{d\tau^2}{8}\right)\,. \label{eq:krange} \end{align}$ であることに注意したい。特に、$k$ は$\tau$が定数の時、$d$について”指数的に大きく”なれる。この補題は、特徴行列に直接関連付けることができる。具体的には、この補題は以下の結果と等価である:

Proposition (JL 特徴行列): JLの補題の様に選ばれた任意の$\tau,d,k$に対して、次を満たす行列$\Phi \in \mathbb{R}^{k\times d}$が任意の$i\in[k]$で存在する。(これよくわかってない…)

\[\begin{align} \max_{i\in [k]} \inf_{\theta\in \mathbb{R}^d} \|\Phi \theta - e_i \|_\infty \le \tau\,, \label{eq:featjl} \end{align}\]

ここで、$e_i$は$\mathbb{R}^k$の標準ユークリッドベクトルの$i$番目の基底ベクトルであり、特に$\varphi_i^\top$が$\Phi$の$i$番目の行のとき、 $|\Phi \varphi_i - e_i|_\infty \le \tau$が成立する。

証明: JLの補題に基づいて、$\Phi$の行として$v_1,\dots,v_k$を選ぶ。$i\in [k]$を固定する。この時、 $\begin{align*} \Phi v_i - e_i = (v_1^\top v_i,\dots,v_i^\top v_i,\dots, v_k^\top v_i)^\top - e_i = (v_1^\top v_i,\dots,0,\dots, v_k^\top v_i)^\top\,. \end{align*}$ である。定義より、$j\ne i$について$|v_j^\top v_i|\leq \tau$なので主張が成立する。 $\qquad \blacksquare$

最後に、Assignment 0のQuestion 6の結果の応用が必要である。この課題では、長さ$k$のバイナリ配列の中の単一の非ゼロの要素を識別する任意のアルゴリズムは、期待値で少なくとも$(k+1)/2-1/k$の要素を見る必要があることの証明を求めた。確率$1/2$でアルゴリズムが正しいことを要求する場合も同様の下限を適用する:

Lemma (高確率針の補題): $p>0$とする。長さ$k$の任意のバイナリ配列の非ゼロの要素を少なくとも$p$の確率で正確に識別する任意のアルゴリズムでは、使用するクエリの期待値は少なくとも$\Omega(p k)$である。

実際、もし確率$p$で正しいアルゴリズムの使用するクエリの最悪のケースの期待値が$q_k$である場合、$k\ge 2$のとき$q_k \ge p( \frac{k+1}{2}-\frac{1}{k})$である。

証明: 省略（課題）。 $\qquad \blacksquare$

以上を使うと、求めたかった定理の証明ができる:

定理の証明: ここでは証明のスケッチだけ示す。

前述の性質を持つプランナー$\mathcal{P}$を固定する。 $k$は後に決める正の整数とする。特徴量マップ$\varphi:\mathcal{S}\times \mathcal{A}\to \mathbb{R}^d$、$k$を準備する。また、状態空間$\mathcal{S}={s,s_{\text{end}}}$と$\mathcal{A}=[k]$行動空間からなる$M_1,\dots,M_k$を考える。ここで$s$はプランナーの初期状態として選ばれており、$s_{\text{end}}$は、報酬ゼロの吸収状態である。 MDPは次に示す同じ決定的な遷移ダイナミクスを共有している： $s$でのすべての行動は、確率1で$s_{\text{end}}$に至り、$s_{\text{end}}$で行われた行動は確率1で$s_{\text{end}}$に至る。また、$s_{\text{end}}$でとった行動の報酬はすべて0である。最後に、MDP $M_i$ の状態 $s$ における報酬を次のように選ぶ:

\[\begin{align*} r_a^{(i)}(s)=\mathbb{I}(a=i) r^*\,, \end{align*}\]

ここで$r^*\in [0,1]$の値は後で選択する。

そして、状態$s$で呼ばれたときにプランナーが返すアクションを$A$とすると、 MDP $M_i$の$s$に誘導される方策の価値は$r^*\mathbb{P}_i(A=i)$であることがわかる。ここで、$\mathbb{P}_i$はプランナーとMDP$M_i$の相互作用で誘導される分布である。したがって、$r^*=2\delta$の場合、最適価値は$2\delta$であり、$\delta$-準最適になるためにはプランナーは$\mathbb{P}_i(A=i)\ge 1/2$となるように$A$を返す必要がある。よって、高確率針の補題により、最低でも$\Omega(k)$の呼び出しが必要となる(呼び出しは確率１で行われるため？)。

最後に、行動価値関数が$q^\pi(s,a)=\mathbb{I}(a=i)r^*$および$q^\pi(s_{\text{end}}, a)=0$の形をとることから、JLの特徴行列構築によってこのMDPの特徴マップを構築することができる?。 $\qquad \blacksquare$

行動数が定数の場合の下限

これまでの結果からは、行動数が固定された場合にクエリ効率的なプランニングが可能かは分からない。これから示すのは、この場合もクエリ効率なプランニングはそんなに簡単ではないということだ。

結果は有限時間 MDPにおけるものだ。 MDP $M=(\mathcal{S},\mathcal{A},P,r)$, 方策 $\pi$, 正の整数 $h>0$ そしてMDPの状態 $s\in \mathcal{S}$ が与えられたとしよう。

\[\begin{align*} v_h^\pi(s) = \mathbb{E}_s^{\pi}[ \sum_{t=0}^{h-1} r_{A_t}(S_t)] \end{align*}\]

を $\pi$ に従って $h$ ステップ行動したときの報酬和と定義する。行動価値関数 $q_h^\pi: \mathcal{S}\times \mathcal{A}\to \mathbb{R}$ も同様に定義する。最適 $h$-ステップ価値関数は

\[\begin{align*} v_h^*(s) = \sup_{\pi} v_h^\pi(s)\,, \qquad s\in \mathcal{S} \end{align*}\]

となる。ベルマン最適作用素 $T: \mathbb{R}^{\mathcal{S}} \to \mathbb{R}^{\mathcal{S}}$ は

\[\begin{align*} T v(s) = \max_{a\in \mathcal{A}} r_a(s) + \langle P_a(s), v \rangle\,. \end{align*}\]

で定義される。メモリレス方策 $\pi$ の方策評価作用素 $T_\pi: \mathbb{R}^{\mathcal{S}} \to \mathbb{R}^{\mathcal{S}}$ は

\[\begin{align*} T_\pi v(s) = \sum_{a\in \mathcal{A}} \pi(a|s) \left( r_a(s) + \langle P_a(s), v \rangle \right) \end{align*}\]

となる。 $v_h^\pi = v_h^*$ が成立するとき、方策 $\pi$ は $h$-ステップ最適であるという。また、 $T_\pi v = T v$ が成立するとき、 $\pi$ は $v:\mathcal{S}\to \mathbb{R}$ に貪欲であるという。次の定理は基本定理に相当する:

定理 (固定時間長版基本定理): $v_0^*\equiv \boldsymbol{0}$ かつ任意の $h\ge 0$ に対して $v_{h+1}^* = T v_h^*$ が成立する。また、各 $i\ge 0$ に対し $\pi_i^*$ が $v_i^*$ に貪欲であるような任意の方策系列 $\pi_0^*,\dots,\pi_h^*, \dots$ を考えると、任意の $h>0$ について $\pi=(\pi_{h-1}^*,\dots,\pi_0^*,\dots)$ (つまり、時刻 $1$ で $\pi_{h-1}^*$ 、時刻 $2$ で $\pi_{h-2}^*$ 、 $\dots$ 、時刻 $h$ で $\pi_0^*$ を用い、その後は任意の行動分布に従う) は $h$-ステップ最適となる:

\[\begin{align*} v_h^{\pi} = v_h^*\,. \end{align*}\]

証明: 証明は読者に任せる。ヒント: 帰納法を用いる。 $\qquad \blacksquare$

この定理において、方策の定義が乱用されていることに注意する。つまり $\pi$ は $h$ ステップ分しか定義されていない点だ。とにかく、この結果に基づくと、固定時間長 $H>0$ に対し、メモリレス方策に相当するのは $H$-ステップ非定常メモリレス方策だ。そのような方策の集合を $\Pi_H$ と記すことにする。

次の結果においては、固定された初期状態 $s_0\in \mathcal{S}$ についてのみの最適性を考える。そして、一般性を失うことなく、 $s_0$ から $h\ge 0$ ステップ後に到達できる状態の集合 $\mathcal{S}_h$ が互いに素であるとする。つまり各 $h\ne h'$ に対し $\mathcal{S}_h\cap \mathcal{S}_{h'}=\emptyset$ (なぜこうしてもよいのか考えてみて欲しい)。このとき、メモリーレス方策 $\pi$ で $s_0$ において最適なものを見つけることができる。つまり、$v^{\pi}_H(s_0)=v_H^*(s_0)$となる。実際、メモリーレス方策で次の等式を全ての $0\le i \le H-1$ に対して同時に満たすものが見つかる。

\[\begin{align} v^{\pi}_{H-i}(s)=v_{H-i}^*(s), \qquad s\in \mathcal{S}_i\,. \end{align}\]

さらに行動価値関数に関しても同様の結果が成り立つ:

\[\begin{align} q^{\pi}_{H-i}(s,a)=q_{H-i}^*(s,a), \qquad s\in \mathcal{S}_i, a\in \mathcal{A}, 0\le i \le H-1\,. \end{align}\]

よって、全ての行動価値関数が特徴写像でよく近似できることに対応する自然な仮定は、特徴写像の列 $(\varphi_h)_{0\le h \le H-1}, \varphi_h: \mathcal{S}_h \times \mathcal{A} \to \mathbb{R}^d$ があり、任意のメモリーレス方策 $\pi$ の $H-h$-ステップ行動価値関数が、 $\mathcal{S}_h$ 上で、 $\varphi_h$ から誘導される基底関数の線形和でよく近似できるという仮定だ。 $\mathcal{S}_h$ 外の状態において $q^{\pi}_{H-h}$ は必要ではないので、 $H-h$-ステップ行動価値関数が $\mathcal{S}_h$** 上に制限されていると今後は仮定する。 $\varphi_h$ から誘導される特徴行列を $\Phi_h$ と書き ($\Phi_h$ の行が各 $\mathcal{S}_{h}\times \mathcal{A}$　の要素に対する特徴ベクトルとなる。ただし、状態行動対の何らかの順番が与えられているとする)、 $\varepsilon^*(M,\Phi)$ 次のように再定義する:

$\begin{align} \varepsilon^*(M,\Phi) : = \sup_{\pi \text{ memoryless}} \max_{0\le h \le H-1}\inf_{\theta\in \mathbb{R}^d} \| \Phi_h \theta - q^{\pi}_{H-h} \|_\infty\,. \end{align}$

今、目的関数を変更したので、 $(\delta,\varepsilon)$-sound ローカルプランナーの定義も次のように変更する必要がある: MDPが $\varepsilon^*(M,\Phi)\le \varepsilon$ を満たすと仮定すると、初期状態 $s_0$ から行動を始めた時の $H$-ステップ無割引総報酬が $\delta$-最適もしくはそれよりよくなる方策を出力する。以降、そのようなプランナーを $H$-ステップ$(\delta,\varepsilon)$-sound と呼ぶ。

この定義を用いて、この節の主となる結果を次のように述べることが出来る:

Theorem (クエリの下界: 行動空間が小さい有限時間MDPの場合): $\varepsilon>0$、$0<\delta\le 1/2$ と正の整数 $d$ に対し、

\[\begin{align*} u(d,\varepsilon,\delta) = \left\lfloor\exp\left(\frac{d (\frac{\varepsilon}{2\delta})^2}{8}\right)\right\rfloor\,. \end{align*}\]

と定義する。任意の $\varepsilon>0$、$0<\delta\le 1/2$、正の整数 $\mathrm{A},\, H,\, d$ で $d\le\mathrm{A}^H$ を満たす、多くとも $\mathrm{A}$ 個の行動を持つMDPに対し $H$-ステップ $(\delta,\varepsilon)$-sound となる任意のローカルプランナー $\mathcal{P}$ を考える。もし $\mathrm{A}^H>u(d,\varepsilon,\delta)$ (“エピソード長が長い”)ならば、報酬が閉区間 $[0,1]$ 内の値をとり $\mathrm{A}$ 個の行動を持つ “featurized-MDP” $(M,\varphi)$で、 $\mathcal{P}$ のシミュレーター $(M,\varphi)$ に対する期待クエリ数が少なくとも

\[\begin{align*} \tilde\Omega\left( \frac{u(d,\varepsilon,\delta)}{d(\varepsilon/\delta)^2}\right)\, \end{align*}\]

となるようなものが存在する。一方、$\mathrm{A}^H>u(d,\varepsilon,\delta)$ でない場合、

\[\begin{align*} \tilde\Omega\left( \frac{\mathrm{A}^H}{ H }\right)\, \end{align*}\]

となるようなものが存在する。

換言すると、エピソード長が十分長い場合には以前と同様の $d$ に対し指数的な下界が存在し、一方エピソード長が短い場合にはエピソード長に対して指数的な下界が存在する。ちなみに、上記の $\tilde\Omega(\cdot)$ という記法は対数的な項に対する依存を省略している。また、 $d\le\mathrm{A}^H$ という条件が妥当であることに注意してほしい: 特徴空間の次元が $\mathrm{A}^H$ と同じ程度だとは考えにくいからだ。(もしそうなら特徴写像を使う必要があまりない)

drawing 証明: 定理の仮定を満たす $\mathcal{P}$ を考え固定する。証明のため、 $k=\mathrm{A}^H$ 個のMDP $M_1,\dots,M_k$ で共通の状態空間 $\mathcal{S} = \cup_{0\le h \le H} \mathcal{A}^h$ と行動空間 $\mathcal{A}$ を持つものを考える。ここで、慣習に従って、$\mathcal{A}^0$ は唯一の要素 $\perp$ からなる単集合とする。 $\perp$ は初期状態 $s_0$ となる。状態遷移確率は全MDPで共通で、以下のものとする: 状態 $s\in \mathcal{S}$ で行動 $a\in \mathcal{A}$ をとると次状態 $s’$ は、$s=\perp$ なら $(a)$、$s \in \mathcal{A}^h, h \neq H$ なら $(a_1,\dots,a_h,a)$、$s \in \mathcal{A}^H$ なら $s$。MDPは報酬関数のみ異なる。報酬関数を説明するため、 $f$ を $[k]$ から $\mathcal{A}^H$ への全単車とする。

$1\le i \le k$ を固定し $(a_0^*,\dots,a_{H-1}^*)$ を $f(i)=(a_0^*,\dots,a_{H-1}^*)$ で定義する。 $s_0^*=s_0$、 $s_1^*=(a_0^*)$、 $s_2^*=(a_0^*,a_1^*)$、$\ldots$、$s_H^*=(a_0^*,\dots,a_{H-1}^*)$ とする。すると、MDP $M_i$ において、 $r_{a_{H-1}^*}(s_{H-1}^*)=2\delta$ でその他の状態行動対に関しては $r_a(s)=0$ となる。

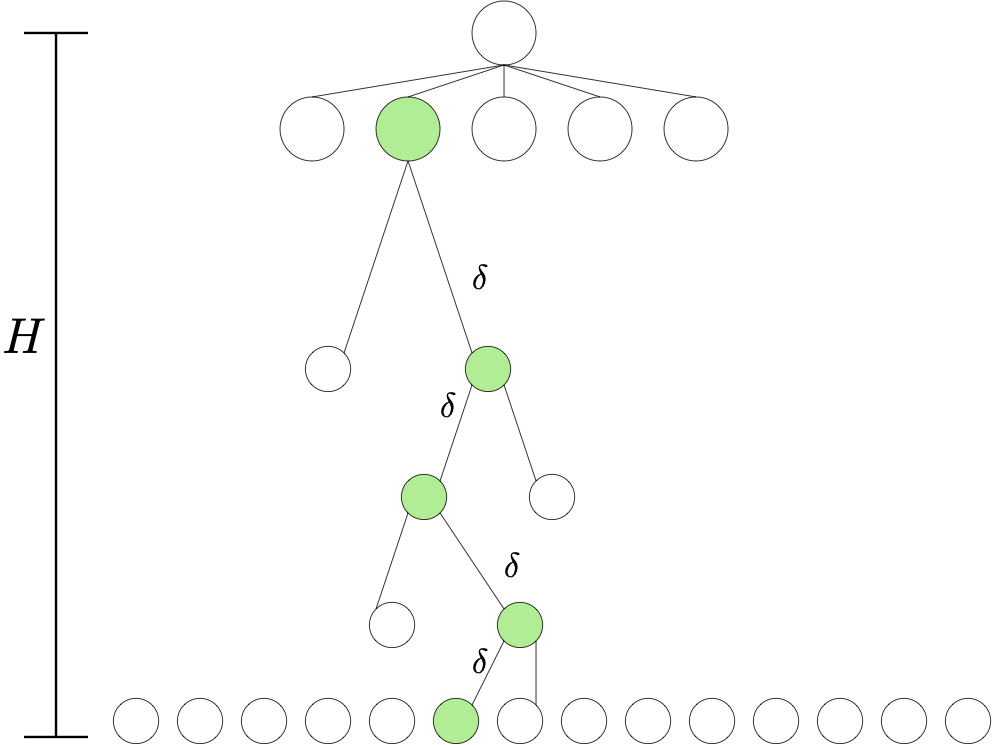
$\perp$ からの最適な $H$-ステップ報酬は $2\delta$ でこれを達成する唯一の方策は状態の系列 $s_0^*,s_1^*,\dots,s_{H-1}^*$ を選ぶもののみであることに注意してほしい。この MDP $M_i$ は右図のように木として表すことができる。図内の緑色のノードが状態の系列 $s_0^*,s_1^*,\dots,s_{H-1}^*,s_H^*$ となる。また $0\le h \le H$ に対し $\mathcal{S}_h = \mathcal{A}^h$ であることにも注意してほしい。

次に、後ほど用いるため、$M_i$ におけるメモリーレス方策の行動価値関数を導出する。 $0\le h \le H-1$ を固定せよ。すると、 $q^{\pi}_{H-h}$ は $\mathcal{S}_h$ 上の関数となる。また、任意の $s\in \mathcal{S}_h (=\mathcal{A}^h)$ と $a\in \mathcal{A}$ に対し、

\[\begin{align} q^\pi_{H-h}(s,a) = \begin{cases} 2\delta\,, & \text{if } h=H-1, s=s_{H-1}^*, a=a_{H-1}^*\,;\\ v^\pi_{H-h-1}(s_{h+1}^*)\,, & \text{if } h<H-1, s=s_h^*, a=a_h^*\,;\\ 0\,, & \text{otherwise}\,. \end{cases} \label{eq:qpiinfh} \end{align}\]

となる。ここで $0\le v^\pi_{H-h-1}(g(s,a))\le 2\delta$ に注意。各ステップ $0\le h \le H-1$ において、 $q^\pi_{H-h}$ の値がゼロでない状態行動対は唯一であること、そしてその値は閉区間 $[0,2\delta]$ 内の値を取ることが分かる。

プランナーは少なくとも $\delta$ 最適なので、プランナーが返す行動 $A$ に対し、 $\mathbb{P}(A\ne a_0^*)\le 1/2$ が成立することが分かる ($a_0^*$ 以外の行動は報酬がゼロなので)。プランナーを新たに $b\ge \log(2H)/\log(2)=\log_2(2H)$ 回呼び出し、この呼び出し中に最も多く返された行動を $A_0$ と定義する。すると $\mathbb{P}(A_0\ne a_0^*)\le 1/(2H)$ が満たされる。これを状態 $S_1=g(s_0,A_0)$ でも行い $A_1$ が得られ、

\[\begin{align*} \mathbb{P}(A_0\ne a_0^* \text{ or } A_1\ne a_1^*) & = \mathbb{P}(A_0\ne a_0^*)+ \mathbb{P}(A_0= a_0^*,A_1\ne a_1^*)\\ & \le \mathbb{P}(A_0\ne a_0^*)+ \mathbb{P}(A_1\ne a_1^*|A_0= a_0^*) \le \frac{1}{2H}+\frac{1}{2H}\,. \end{align*}\]

となる。これを状態 $S_2 = g(S_1,A_1)$ とそれ以降の状態でも行い、最終的に行動の系列 $A_0,\dots,A_{H-1}$ で $\mathbb{P}(A_0\ne a_0^* \text{ or } \dots \text{ or } A_{H-1}\ne a_{H-1}^*)\le 1/2$ となるものが得られる。

以前用いた論法により (“針探し”問題への還元)、このプロセスは全体で $\Omega(k)$ 回のクエリを必要とする。 $\mathcal{P}$ の用いた期待クエリ数を $q$ とすると、期待クエリ数は $H \log_2(2H) q$。よって、

\[q = \Omega\left( \frac{k}{\log_2(2H)H} \right)\]

となる。次に $\Phi = (\Phi_h)_{0\le h \le H-1}$ を $\varepsilon^*(M,\Phi)\le \varepsilon$ となるように選ぼう。 $\Phi_h$ に対し、 “JL特徴行列” $\tilde \Phi_h\in \mathbb{R}^{|\mathcal{S}_h| \times d}$ を Eq. \eqref{eq:featjl} が成立するように選ぶ。そして $\Phi_h = \sqrt{2\delta} \tilde \Phi_h$ とする。 $h<H-1$ に対して $\theta_h = v^\pi_{H-h-1}( s_{h+1}^* ) \varphi_h( s_h^*,a_{h}^* )/(2\delta)$ とし、 $h=H$ に対しては $\theta_h = \varphi_h( s_h^*,a_{h}^* )$とする。すると、Eq. \eqref{eq:qpiinfh} より、 $(s,a)\ne (s_h^*,a_{h}^*)$ に対して $|\varphi_h(s,a)^\top \theta_h-q_{H-h}(s,a)| \le |v^\pi( s_{h+1}^* )| \, |\tilde \varphi_h(s,a)^\top \tilde \varphi_h(s_h^*,a_{h}^*)|\le 2\delta \tau$ かつ、 $(s,a)=(s_h^*,a_{h}^*)$ に対して $\varphi_h(s,a)^\top \theta_h=q_{H-h}(s,a)$ となる。よって、 $\varepsilon^*(M,\Phi)\le \varepsilon$ holds if we set $\tau=\varepsilon/(2\delta)$が得られる。

Eq. \eqref{eq:krange} より、もし $d\le k$ ならば $\tilde \Phi_h$ が存在し、また

\[\begin{align*} k \le u:=\left\lfloor\exp\left(\frac{d (\frac{\varepsilon}{2\delta})^2}{8}\right)\right\rfloor \end{align*}\]

となる。

$k = \mathrm{A}^H$ だったので、 $\mathrm{A}^H\le u$ (“エピソード長が短い場合”) の場合の命題は示された。逆の場合 (“エピソード長が長い場合”)には、 $\tilde H$ を $\mathrm{A}^{\tilde H}\le u$ を満たす最大の整数とし、上記と同じ論法をエピソード長 $\tilde H$ として用いることで次の下界を得る:

$q = \Omega\left( \frac{\mathrm{A}^{\tilde H}}{\log_2(2\tilde H)\tilde H} \right) = \Omega\left( \frac{u}{\log_2(2\tilde H)\tilde H} \right)\,.$ これで証明が終わる。 $\qquad \blacksquare$

Notes

割引報酬和の場合の下界はプランニングホライゾンを持たない。有限エピソード長の場合もエピソード長が長い場合にはホライゾンに依存しない。Eq. \eqref{eq:limit}内の余分な “ホライゾン項” が必要なのかは分かってない。
どちらの場合も結論は、もし”かなりよい特徴写像”を持っていたとしても、高精度のプランニングは不可能であるということだ。
TCSに詳しい読者は、ここで我々が考えた問題が、“fully polynomial time approximation schemes” (FPTAS) の存在性に関する問題に似ていることに気づくかもしれない。
プランニングに関して解かれていない問題は多く存在する。例えば、二つ目の定理に相当するものはが割引報酬和の設定でも存在するのだろうか?

Bibliographical notes

Johnson-Lindenstraussの補題をこのように用いるのは Du, Kakade, Wang and Yang のアイデアによる。一つ目の定理は this paper 内の結果の変形である。二つ目の定理は上記 Du et al. 内の Theorem 4.1 を変形したものである。論文内ではグローバルプランニングにおける同様の結果を示している。

Johnson-Lindenstraussの補題は彼らによる。証明は確率的方法を用いており、例えば

Dasgupta, Sanjoy; Gupta, Anupam (2003), “An elementary proof of a theorem of Johnson and Lindenstrauss” link, Random Structures & Algorithms, 22 (1): 60–65

にある。