4. 方策反復法

この講義では、

1. 方策反復法を定義し、
2. 方策反復法が $\tilde O( \textrm{poly}(\mathrm{S},\mathrm{A}, \frac{1}{1-\gamma}))$ の計算コストで最適方策に至る

ことを見ていく。 2の計算コストを前回解説した価値反復法の計算コストと比較してみよう。 前回の講義では、最適価値関数との誤差を$\delta$とすると、価値反復法が$\log(1/\delta)$に比例して計算コストが大きくなることを学んだ。 これは$\delta\to 0$のとき方策反復法の計算コストと大きく異なる。 この場合、価値反復法は方策反復法より劣っていることになるが、本当にそうなのだろうか？ 本講義の最後にこれについて議論する。

方策反復法

方策反復法はまず任意の決定的な(メモリーレス)方策\(\pi_0\)で初期化をする。 続いて、ステップ$k=0,1,2,\dots$にて次の処理を行う:

1. \(v^{\pi_k}\)を計算する
2. \(v^{\pi_k}\) について貪欲な決定的方策 \(\pi_{k+1}\)を計算する

$v^{\pi_k}$はどうやって計算するのだろうか? $v^{\pi}$は任意のメモリーレス方策$\pi$と作用素$T_\pi$について、$v^\pi = T_\pi v^\pi$の不動点であることを思い出そう。 また、任意の $v\in \mathbb{R}^{\mathcal{S}}$ について $T_\pi v = r_\pi + \gamma P_\pi v$ であったことを思い出して欲しい。 この時、$v^\pi = T_\pi v^\pi$ は$v^\pi$についての線形な連立方程式であり、解析的に解くことができる。 方策反復法では、以下のように$v^{\pi_k}​$を求める。 \(\begin{align} v^{\pi_k} = (I - \gamma P_{\pi_k})^{-1} r_{\pi_k}\,. \label{eq:vpiinv} \end{align}\)

勘の良い読者は $I-\gamma P_{\pi_k}$ の逆行列がなぜ常に存在するか気になるだろう。 これが well-defined である理由は色々なやり方で説明できる。 例えば、正方行列$A$の全ての固有値が複素数平面の単位円内に存在する時、$(I-A)^{-1} = \sum_{i\ge 0} A^i$ が成立することを利用すると説明できる。 これはノイマン級数による$I-A$の展開として知られている。 名前は難しそうだが、これは高校生で学ぶ $|x|<1$についての初歩的な等比級数の式 $1/(1-x) = \sum_{i\ge 0} x^i$とやっていることは同じである¹。

式 \(\eqref{eq:vpiinv}​\) より、\(v^{\pi_k}​\) は最大で\(O( \mathrm{S}^3 )​\) の代数計算で求まることが分かる(実際、最大で\(O( \mathrm{S}^{2.373\dots})​\)で済む ). $r_{\pi_k}​$の計算コストは($\pi_k​$は決定的なので)$O(\mathrm{S})​$であり、ランダムにテーブルにアクセスできるMDPにおいて、$P_{\pi_k}​$の計算コストは$O(\mathrm{S}^2)​$である。 ここでの計算コストは行動の数とは関係ないことに注意したい。

貪欲な方策を計算するステップでは、それぞれの状態$s\in \mathcal{S}$において$v^{\pi_k}$についてのベルマン先読みを最大にする行動を計算する。 これは定式化すると以下の最大化問題を解くことになる。

\[\max_{a\in \mathcal{A}} r_a(s) + \gamma \langle P_a(s),v^{\pi_k} \rangle\]

これを解いて得られる行動を保存し、$\pi_{k+1}​$で選択する。 全ての方策は決定的であるため、ある状態では保存された行動のみ選択するとすれば、状態毎に確率ベクトルを保持する場合よりもメモリを効率化できる(確率ベクトルを保持する場合、選択しない行動について余計な0要素を保持する必要がある)。 これに合わせて表記を簡便化するため、決定的なメモリーレス方策を$\mathcal{S} \to \mathcal{A}​$なる写像とする。つまり、$\pi_{k+1}: \mathcal{S} \to \mathcal{A}​$である。

$v^{\pi_k}​$は長さ$\mathrm{S}​$のベクトルであるため、それぞれについて最大値を評価するコストは$O(\mathrm{S})​$である。 よって、最大値を計算するコスト全体は$O(\mathrm{S}\mathrm{A})​$であり、ここで計算コストに行動の数が現れる。

本講義の一番大事な結果は、方策反復法が$\tilde O( \mathrm{SA}/(1-\gamma))$回の更新で必ず最適な方策に至るという定理である(これは近似最適ではない！)。 この結果の証明に大事なポイントは以下の二つである:

1. 方策反復法は指数的に収束する
2. $H_{\gamma,1}​$ 回更新する毎に、方策反復法はどこかの状態で準最適な行動を一つ以上取り除く

最初の結果は方策反復法を価値反復法と比較することで得られる。 価値反復法は初期条件によらずに指数レートで収束することを思い出そう。 そのため、 \(\| v^{\pi_k}-v^* \|_\infty \le \| T^k v^{\pi_0}-v^* \|_\infty​\) が証明できればよい。 実際、方策改善定理として知られる定理で、 \(\begin{align} T^k v^{\pi_0} \le v^{\pi_{k}}\,, \qquad k=0,1,2,\dots\, \label{eq:pilk} \end{align}\)

なる指数レートよりも早く収束することを示唆する結果が得られる。

---

補題 (指数的方策改善定理): $\pi,\pi’$を、$\pi’$が$v^\pi​$についての貪欲であるようなメモリーレス方策とする。 このとき、以下が成立する。 \(\begin{align*} v^\pi \le T v^{\pi} \le v^{\pi'}\,. \end{align*}\)

---

証明:

まず、定義から $T v^\pi = T_{\pi’} v^\pi$ が成り立つ。 また、$v^\pi = T_\pi v^\pi \le T v^\pi$ も成立する。 これらを合わせると、

\[\begin{align} v^\pi \le T v^{\pi} = T_{\pi'} v^{\pi}\,. \label{eq:pilemmabase} \end{align}\]

が成立する。

証明は次の式について、$i\ge 1​$への帰納法によって示す:

\[\begin{align} v^\pi \le T v^{\pi} \le T_{\pi'}^i v^{\pi}\,. \label{eq:pilemmainduction} \end{align}\]

これが示せれば、両辺について$i\to \infty​$を取れば証明できる。

$i=1​$の場合はすでに示した。 それ以外の場合について、まず式\(\eqref{eq:pilemmainduction}​\)が$i\ge 1​$で成立すると仮定しよう。 $i+1​$でも成立することを示すため、$T_{\pi’}​$を式\(\eqref{eq:pilemmainduction}​\)の両辺に適用する。 $T_{\pi’}​$は単調なので、次が成立する。 \(\begin{align*} T_{\pi'} v^\pi \le T_{\pi'}^{i+1} v^{\pi}\,. \end{align*}\)

これを式\(\eqref{eq:pilemmabase}​\)と合わせると、

\[\begin{align*} v^\pi \le T v^\pi = T_{\pi'} v^\pi \le T_{\pi'}^{i+1} v^{\pi}\,, \end{align*}\]

を得る。これで証明できた。 \(\qquad \blacksquare\)

この補題は価値関数が単調増加であることを示している。 この補題を$\pi = \pi_0​$から始めて$k​$回適用すると式\(\eqref{eq:pilk}​\)が得られ、また、次の結果が得られる。

---

系 (指数収束): \(\{\pi_k\}_{k\ge 0}\)を方策反復法で生成される方策の系列とする。この時、任意の\(k\ge 0​\)について次が成り立つ。 \(\begin{align} \|v^{\pi_k} - v^*\|_\infty \leq \gamma^k \|v^{\pi_0} - v^*\|_\infty\,. \label{eq:pig} \end{align}\)

---

証明: 式\(\eqref{eq:pilk}\)より、 \(T^k v^{\pi_0} \le v^{\pi_k} \le v^*\,, \qquad k=0,1,2,\dots\,.\)

が成立し、次も成り立つ。

\[v^* - v^{\pi_k} \le v^* - T^k v^{\pi_0}\,, \qquad k=0,1,2,\dots\,.\]

上式について、要素ごとの絶対値を取り、状態についての最大値を取ると、

\[\|v^* - v^{\pi_k}\|_\infty \le \|v^* - T^k v^{\pi_0}\|_\infty = \|T^k v^* - T^k v^{\pi_0}\|_\infty \le \gamma^k \|v^* - v^{\pi_0}\|_\infty\,,\]

となり、所望の結果を得た。 上の不等式では基本定理を利用しており、また、最後の不等式では$T$が$\gamma$-縮小であることを利用した。 \(\qquad\blacksquare\)

ここで、次の”厳密向上定理?”を示そう。 証明にはここまでで導出した補題?を利用するが、新しいテクニックも使う。

---

補題 (狭改善定理): $\pi_0$を任意の準最適なメモリーレス方策、\(\{\pi_k\}_{k\ge 0}\)を方策反復法で得られた方策の系列とする。 このとき、任意の$k\ge k^*:= \lceil H_{\gamma,1} \rceil +1$について、次を満たす状態$s_0\in \mathcal{S}$が存在する。

\[\pi_k(s_0)\ne \pi_0(s_0)\,.\]

---

この補題は\(k^* = \tilde O \left( \frac{1}{1-\gamma}\right) ​\)回の更新毎に、準最適行動がなくなるまで、方策反復法がどこかの状態で行動を除去し続けることを意味している。 全ての状態で少なくとも1つの行動が最適になり、最適方策は除去しないため、この操作は最大で$S(A-1) = SA-S​$回実行される。 この向上定理から本講義で目指していた結果が得られる。

---

定理（方策反復法の計算コスト）： 

報酬が$[0,1]​$の有限な割引MDPを考える。 \(k^*​\)を向上定理と同様に定義し、\(\{\pi_k\}_{k\ge 0}​\)を任意の方策$\pi_0​$で初期化し、方策反復法によって得られた方策の系列とする。 この時、最大で \(k= k^* (\mathrm{S}\mathrm{A}-\mathrm{S}) = \tilde O\left( \frac{\mathrm{S}\mathrm{A}-\mathrm{S} }{1-\gamma } \right)\) の更新で、方策$\pi_k$は$v^{\pi_k}=v^*$となり、最適になる。 つまり、方策反復法は最大で \(\tilde O\left( \frac{ \mathrm{S}^4 \mathrm{A} +\mathrm{S}^3{\mathrm{A}^2} }{1-\gamma} \right)\) の算術論理演算によって計算される。

---

これから、改善定理の証明に入る。 まずこの定理を証明するために便利な方程式を見ていこう。 この方程式は価値差分方程式?と呼ばれ、2つのメモリーレス方策の価値関数の差分を表すことができる。 $\pi, \pi’$を2つのメモリーレス方策とする。 $v^{\pi’} = (I-\gamma P_{\pi’})^{-1} r_{\pi’}​$であることを思い出すと、代数計算により、 \(\begin{align*} v^{\pi'} - v^{\pi} & = (I-\gamma P_{\pi'})^{-1} [ r_{\pi'} - (I-\gamma P_{\pi'}) v^\pi] \\ & = (I-\gamma P_{\pi'})^{-1} [ T_{\pi'} v^\pi - v^\pi]\,. \end{align*}\)

を得る。

ここで、

\[g(\pi',\pi) = T_{\pi'} v^\pi - v^\pi\,,\]

なる表記を導入する。これは$\pi’$の$\pi$に対する”アドバンテージ”とみなせる。 この時、次の補題を得る:

---

補題 (価値差分方程式): 任意のメモリーレス方策\(\pi, \pi'\)について、次が成り立つ。

\[v^{\pi'} - v^\pi = (I - \gamma P_{\pi'})^{-1} g(\pi',\pi)\,.\]

---

もちろん、対称的な関係も成り立つ。

これを使うと、向上定理を示すことができる。 \(\pi^*\)は最適なメモリーレス方策なので、任意のメモリーレス方策$\pi$について、\(g(\pi,\pi^*)\le 0\)が成り立つ。 また、この逆も成り立つことに注意しよう。つまり、\(g(\pi,\pi^*)\le 0\)が任意の$\pi$について成り立つなら、$\pi^*$は最適である。 このことから、\(-g(\pi_k,\pi^*)\)が方策反復法における進捗状況を把握するための理想的な指標であることが分かる。 方策反復法では、これが高い値から始まり、$k$の増加に対して減少するのが望ましい。

特に、

\[\begin{align} -g(\pi_k,\pi^*)(s_0)<-g(\pi_0,\pi^*)(s_0) \label{eq:strictprogress} \end{align}\]

が、ある状態$s_0\in \mathcal{S}$で成り立つ時、代数的に

\[r_{\pi_k(s_0)}(s_0) + \gamma \langle P_{\pi_k(s_0)} , v^* \rangle > r_{\pi_0(s_0)}(s_0) + \gamma \langle P_{\pi_0(s_0)} , v^* \rangle\]

が成り立ち、$\pi_k(s_0)\ne \pi_0(s_0)$が成立する。 よって式\(\eqref{eq:strictprogress}\)が任意の$k\ge k^*$について成立することを示せば、向上定理は証明できる。

証明 (改善定理): $k\ge 0$と最適でない\(\pi_0\)を定義する?。 \(\pi^*\)を任意の最適なメモリーレス方策とする。 この時、方策\(\pi_k\)について価値差分方程式と\(\pi^*\)が最適であることから、

\[- g(\pi_k,\pi^*) = (I - \gamma P_{\pi_k}) (v^* - v^{\pi_k}) = (v^* - v^{\pi_k}) - \gamma P_{\pi_k} (v^* - v^{\pi_k}) \leq v^* - v^{\pi_k}\,\]

が成り立つ。最後の不等式は\(v^* - v^{\pi_k}\ge 0​\)および$P_{\pi_k}​$が確率的であり単調性を持つためである。 後は右辺を\(-g(\pi_0,\pi^*)​\)と比較すれば我々の目的は達成される。 式\(\eqref{eq:pig}​\)によって右辺を\(v^*-v^{\pi_0}​\)と比較でき、価値差分方程式によって\(-g(\pi_0,\pi^*)​\)と比較できるので、式\(\eqref{eq:pig}​\)を使う準備が整う。 まず、上の不等式について最大値ノルムを両辺に取る(最大値ノルムは不等式の関係を保持することに注意)。 続いて、式\(\eqref{eq:pig}​\)と価値差分方程式により、以下を得る。 \(\begin{align} \|g(\pi_k,\pi^*)\|_\infty & \leq \|v^* - v^{\pi_k}\|_\infty \leq \gamma^k \|v^* - v^{\pi_0}\|_\infty = \gamma^k \|(I - \gamma P_{\pi_0})^{-1} (-g(\pi_0,\pi^*))\|_\infty \nonumber \\ & \leq \frac{\gamma^k}{1 - \gamma} \|g(\pi_0,\pi^*)\|_\infty\,, \label{eq:plmain} \end{align}\)

ここで、最後の不等式は \((I - \gamma P_{\pi_0})^{-1} = \sum_{i\ge 0} \gamma^i P_{\pi_0}^i​\) を利用しており、三角不等式と\(P_{\pi_0}​\)が最大値ノルムについて「non-expansion」であるため、 \(\| (I - \gamma P_{\pi_0})^{-1} x \|_\infty \le \frac{1}{1-\gamma}\| x \|_\infty​\) が任意の\(x\in \mathbb{R}^{\mathrm{S}}​\)で成立する。

ここで、$s_0\in \mathcal{S}$を\(-g(\pi_0,\pi^*)(s_0) = \| g(\pi_0,\pi^*)(s_0)\|_\infty\)を満たす状態とする ($\mathcal{S}$は有限なので、これは存在する)。 \(0\le -g(\pi_k,\pi^*)(s_0)\le \| g(\pi_k,\pi^*)\|_\infty\) とすると、式\(\eqref{eq:plmain}\)より \(-g(\pi_k,\pi^*)(s_0) \leq \|g(\pi_k,\pi^*)\|_\infty \leq \frac{\gamma^k}{1 - \gamma} (-g(\pi_0,\pi^*)(s_0)).\) を得る。

ここで、\(k\ge k^*\)なら、\(\frac{\gamma^k}{1 - \gamma} < 1\)である。 \(\pi_0 \neq \pi^*\)なので、\(0<\|g(\pi_0,\pi^*)\|_\infty = -g(\pi_0,\pi^*)(s_0)\) が成り立ち、

\[\begin{align*} -g(\pi_k,\pi^*)(s_0) \leq \frac{\gamma^k}{1 - \gamma} (-g(\pi_0,\pi^*)(s_0)) < -g(\pi_0,\pi^*)(s_0)\,, \end{align*}\]

によって式\(\eqref{eq:strictprogress}​\)が成立するため、上述より、\(\pi_k(s_0)\ne \pi_0(s_0)​\)が成立する。 これは任意の\(k\ge k^*​\)で成立するため、以上で証明が完了した。 \(\qquad\blacksquare​\)

価値反復法は方策反復法より劣っているのか？

第3回の講義で価値反復法の計算コストには $\log(1/\delta)$ の項が含まれていることを確認した。この項は、要求される精度 $\delta$ がゼロに近づくにつれ際限なく大きくなる。しかしながら、現段階ではこの項が曖昧に解析した結果（the result of a loose analysis）なのか価値反復法の性質なのか定かではない。

価値反復法は、全ての価値関数が $[0,1/(1-\gamma)]​$ の値をとるという仮定のもとで $\mathrm{S}​$, $\mathrm{A}​$ , プランニングホライゾン $1/(1-\gamma)​$ に比例する計算コストにより最適方策を見つけられると保証できるのだろうか？

上記を達成する全てのアルゴリズムを強多項式と呼ぶとすると、方策反復は強多項式アルゴリズムであると言える。ただし、上記の定義においては、報酬が $[0,1]​$ の範囲であるという仮定ではなく、価値関数の取り得る範囲が $[0,1/(1-\gamma)]​$ という仮定であることに注意したい。これはより弱い仮定であるが、方策反復の計算コストに関する証明を確認するとこの仮定のみが必要であることが分かる。

しかしながら、次の命題から価値反復法は強多項式ではないことが分かる。

---

命題：

状態遷移が決定的であり、任意の方策で価値関数が $[0,1/(1-\gamma)]$ の値をとり、状態が3つ、行動が2つであるようなMDPsを考える。このとき、最適方策を得るための価値反復の反復複雑度の最悪ケースが無限大であるMDPsが存在する。

---

ここで、反復複雑度とは、価値反復法によって方策 $\pi_k​$ が最適方策に至るために必要な最小の反復回数 $k​$ を指す。もちろん、反復複雑度が無限大であることは計算コストが無限大であることを指す。

証明: 下の図に該当するMDPを示す：

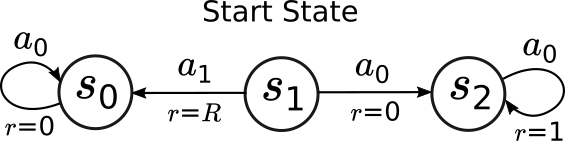
図中のMDPにおいて、状態とその名前を円で示し、矢印で行動 $a_0,a_1$ を取ったときの状態遷移の結果を示す。 $r=\cdot$ は遷移において得られる報酬を示す。ただし、 $R$ はリターンではなく、$[0,\gamma/(1-\gamma)]$ から選ばれるパラメータであり、これにより価値反復の反復複雑度が決まる。

この例では、状態価値は $v_0 = \boldsymbol{0}$ で初期化されるとする。 状態 $s_1$ において、最適な行動が $a_0$ であることは容易に分かり、この状態における状態価値は $\gamma/(1-\gamma)$ となる。 また、$\pi_0(s_1)=a_1\ne a_0$ であることも容易に分かる。 ここで、 $R$ が $\gamma/(1-\gamma)$ に近づくにつれ、価値反復が状態 $s_1$ （原版では $s_0$ だが多分typo）で行動 $a_1$ を選択することを確認する。そのため、まず $k\ge 0$ において $v_k(s_0)=0$, $v_k(s_2) =\frac{1}{1-\gamma}(1-\gamma^k)$ であることを確認する。 次に、 $R>v_k(s_2)$ のとき $\pi_k(s_1)=a_1$ であることが分かる。 以上から、もし価値反復に $k_0$ 以上の回数の反復をさせたい場合、 $R = \frac{v^*(s_2)+v_{k_0}(s_2)}{2}<\gamma/(1-\gamma)$ にすれば良い。 \(\blacksquare\)

方策反復がどのように反復回数の発散を避けているのかを考えることは示唆的である。 上の例では、最適方策を計算することを考えていたので、価値反復は明らかに方策反復に劣っていることが分かった。 しかしながら、第3回の講義では価値反復によりせいぜい $\log(1/\delta)$ （と他の項の掛け算）の計算コストで $\delta$ 最適な方策を得られるという良い結果が得られている。

これは一体何を意味するのだろうか。我々は価値反復を厳密に計算するための計算コストが有限ではないことを本当に気にする必要があるのだろうか。厳密な計算を気にしなくて良い理由はたくさんある。結局のところ、我々はサンプリングや学習など、厳密に計算できないような処理を行うだろう。加えて、我々のモデルは単なるモデルであることを思い出して欲しい。つまり、モデルそのものが誤差を生み出す要因となる。これらを踏まえ、なぜ我々は厳密に計算することを気にする必要があるのだろうか。まとめると：

厳密な最適性があることは良いことだが、要求される精度に応じて緩やかに計算コストが大きくなるような近似計算もまた許容されるはずである。

しかし、方策反復が適切な解をどのように「得て」、わずか数行のコードを変更するだけで計算コストを劇的に改善できることを考えることは依然として興味をそそられる。我々はあるアルゴリズムが証明できる形で他のアルゴリズムに対して優位性があるか、という問いにいつでも立ち返るだろう。もしこれが示せたなら、本当の勝利と言える。つまり、我々はその優位性のあるアルゴリズムより劣っているアルゴリズムを考えなくてよくなる。これはとても素晴らしいことだが、その優劣はどのように問題が定義されたかに依存することを思い出して欲しい。今まで、そしてこれから何度も確認するように、問題設定を変えることによってどのアルゴリズムが適切か否かが劇的に変わる可能性がある。そして、どのアルゴリズムがどういった文脈で他のアルゴリズムに対して優位性があるかなど、誰に分かるのだろうか。

Notes

方策反復の計算コストのバウンド

$\text{poly}(\mathrm{S},\mathrm{A},\frac{1}{1-\gamma})$ 回数の算術・論理演算で最適方策が見つかることを最初に示したのは Yinyu Ye (2011) である。これは当時としては画期的なことだった。我々が示した定理は Bruno Scherrer (2016) に基づいている。この証明は Yinyu Ye のものより容易であるが、主なアイデアは Yinyu Ye で示されたものである。

価値反復の計算コスト

価値反復が強多項式ではないことを示した例は Eugene A. Feinberg, Jefferson Huang and Bruno Scherrer (2014) から引用した。

価値関数が等しくなる場合の停止条件

上記の問題にあるように、2つの行動が同じ数値で最大値になることは読者が想像する以上に多く発生する。この場合、どちらの行動を選択すれば良いだろうか。これは、$\pi_{k+1}=\pi_k​$ を検出したときにアルゴリズムを停止させるような停止条件を用いたいときに問題となる。この停止条件は $O(\mathrm{S})​$ の計算コストが必要であり、コストとしてはとても小さい。 もしこのような停止条件を使いたい場合、システマチックな方法である行動を優先的に選ぶ方法があることを確認しておくべきである。さもなければ、ある状態 $s​$ において方策 \(\pi_k​\) により生成される2つの最適行動があった場合に、$\pi_{k+1}​$ が \(\pi_k​\) が選ばなかった方の最適行動を選び、 $\pi_{k+2}​$ が $\pi_{k}​$ と同じ行動を選ぶ可能性があり、これらの方策が最適であることを検知する停止条件が失敗してしまう。

他の方法でシステマチックにこの問題を解決する方法は、停止条件を変更し、$v^{\pi_k} = v^{\pi_{k+1}}​$ が成立するかを確認する方法である。読者はこれが動作することを確かめて欲しい。 「実用的」には、$v^{\pi_k}​$ と $v^{\pi_{k+1}}​$ が有限の精度で計算される時に計算誤差が乗ってしまうのでこれもまた問題となりえる。こういったことは起こるのだろうか？起こりうるのである！$r_{\pi_k}\ne r_{\pi_{k+1}}​$ でかつ $I-\gamma P_{\pi_k} \ne I-\gamma P_{\pi_{k+1}}​$ であっても、（精度が無限の場合に） $v^{\pi_k} = v^{\pi_{k+1}}​$ になり得る。有限の計算精度の場合、この2つの状態で同じ結果を得ることの保証は全くない！有限精度での計算において保証されていることは同じ入力に対して同じ出力が返ってくるということだけである。

もちろん、この問題に対する簡単な解決策は、上記の定理を用いて反復回数が十分に大きくなったところで止めることである。しかしながら、これは必要以上に無駄な計算をすることになるかもしれない。

References

• Feinberg, E. A., Huang, J., & Scherrer, B. (2014). Modified policy iteration algorithms are not strongly polynomial for discounted dynamic programming. Operations Research Letters, 42(6-7), 429-431. [link]
• Scherrer, B. (2016). Improved and generalized upper bounds on the complexity of policy iteration. Mathematics of Operations Research, 41(3), 758-774. [link]
• Ye, Y. (2011). The simplex and policy-iteration methods are strongly polynomial for the Markov decision problem with a fixed discount rate. Mathematics of Operations Research, 36(4), 593-603. [link]

翻訳者注

---