7. 関数近似

前回の講義で計算したローカルプランナーの下界は、以下の3つの要求を満たしつつ、全てのMDPにおいて良い方策を導くローカルプランナーは存在しないことを示している。

プランナーを用いた方策が全てのMDPのうちいくらかの割合で最適なものとなる (the planner induces policies that achieve some positive fraction of the optimal value in all MDPs;)
状態毎の計算量がプラニングホライゾン$H$に多項式オーダーで依存する
行動の数に多項式オーダーで依存する
MDPの状態の数に依存しない

したがって、これらの要求の一つを諦める以外に選択肢はない。効率性は明らかに譲れない（さもなくばプランナーは役に立たない）ので、代替できる唯一の要求は最初のものとなる。そこで、以下では、この最初の要求を緩和する方法を考える。

以降、プランナーが動作し得るMDPの集合を基本的に制限して要求を緩和しつつ、どのMDPも除外しないような方法を考える。これを達成するため、プランナーにMDPに関する追加のヒントを与え、そのヒントが正しい時だけ良い性能を達成できることを要求する。ヒントは一般的な形式であるため、あるヒントは全てのMDPにおいて正しいものとなる。このようにして、MDPを取り残すことなく、プランナーに効率的かつ効果的であることを要求することができる。

価値関数に対するヒント

まず初めに、価値関数に関するヒントを考える。特に、そのヒントによって最適価値、または全ての方策における価値関数のいずれかが効果的に圧縮可能であることを述べる。

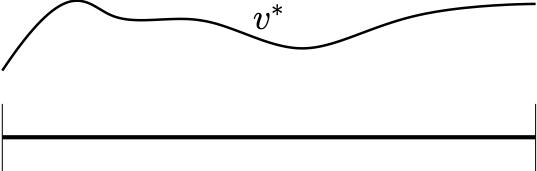drawing 動機付けのために、右の図を考えてみる。あるMDPにおける状態空間が図下の実線の区間で、最適価値関数が図上の曲線のようになっているとする。図から、状態空間において価値関数が滑らかな関数となっていることが分かる。このような比較的ゆっくりと変化する関数は、適当な多項式やフーリエ基底のようないくつかの固定基底関数の線形和や、スプラインを用いることでよく近似できることが知られている。したがって、状態空間が大きく、この例のように無限である場合においても、ホライゾンや行動数、いくつかの係数を得るための計算が多項式に依存する計算量で $v^*$ の良い近似を得ることができるかもしれないと期待される。 $v^*$ が既知であり、MDPシミュレータへアクセスできるとすると、1ステップ先読みをすることにより良い行動を効率的に計算することができる。

線形関数近似

前述の基底関数を $\phi_1,\dots,\phi_d: \mathcal{S} \to \mathbb{R}$ であるとすると、形式的には、いくつかの係数 $\theta =(\theta_1,\dots,\theta_d)^\top\in \mathbb{R}^d$ を用いて最適価値関数を表現できることが期待される。 $\begin{align} v^*(s) = \sum_{i=1}^d \theta_i \phi_i(s)\, \qquad \text{for all } s\in \mathcal{S}\,. \label{eq:vstr} \end{align}$

強化学習の文脈では、ベクトル $(\phi_1(s), \dots, \phi_d(s))^\top$ は状態 $s$ に関する特徴量ベクトルと呼ばれる。よりコンパクトな表記をすると、$\phi$ を状態空間 $\mathcal{S}$ から特徴量空間 $\mathbb{R}^d$ への写像と考え、 $\phi(s) = (\phi_1(s),\dots,\phi_d(s))^\top\,.$

逆に、$\phi: \mathcal{S}\to \mathbb{R}^d$ が与えられた時に、その要素は $\phi_1,\dots,\phi_d$ を用いて表現できる。また、次のように行列形式での表記を用いることも便利である。状態の数が $\mathrm{S}$ であったことを思い出すと、一般性を損なうことなく $\mathcal{S} = [\mathrm{S}]$ と仮定できる。次に、 $\phi_1,\dots,\phi_d$ を$\mathrm{S}$次元のベクトルと扱うことができる。ここで、$\phi_j$ の $i$ 番目の要素は $\phi_j(i)$ と表す。さらに、 $\phi_1,\dots,\phi_d$ をスタックして行列形式で表すことができる。 $\Phi = \begin{pmatrix} | & | & \dots & | \\ \phi_1 & \phi_2 & \dots & \phi_d \\ | & | & \dots & | \end{pmatrix} \in \mathrm{R}^{\mathrm{S}\times d}\,.$

このように、 $\Phi$ は $\mathrm{S}\times d$ の行列となる。基底関数の線形結合で記述できる状態空間上の実数関数の集合は以下となる。 $\mathcal{F} = \{ f: \mathcal{S} \to \mathbb{R} \,:\, \exists \theta\in \mathbb{R}^d \text{ s.t. } f(s) = \langle \phi(s),\theta \rangle \}\,.$

実数関数空間とベクトル空間 $\mathbb{R}^{\mathrm{S}}$ を自然な形で同一視すると、$\mathcal{F}$ は $\mathbb{R}^{\mathrm{S}}$ の $d$ 次元の部分空間であり、$\Phi$ の列空間、またはスパン（列ベクトルの線型結合としてあり得るすべてのもの）、または値域空間と同じであることがわかる。 $\mathcal{F} = \{ \Phi \theta \,:\, \theta\in \mathbb{R}^d \} = \text{span}(\Phi)$

$\mathcal{F}$ が特徴量に依存していることを強調したい場合は、$\mathcal{F}_{\phi}$ や $\mathcal{F}_{\Phi}$と書く。

以上により、基底関数 $\phi_1,\dots,\phi_d$ を指定する方法、特徴マップ $\phi$ を指定する方法、特徴行列 $\Phi$ を指定する方法の3つの同等の方法を紹介し、特徴の線形結合で得られる関数を指定する方法の4つの方法を紹介した。

ヒントの伝え方

上記の問題設定では、プランナーが何らかの方法で特徴量マップを利用できることが暗黙の前提となっていることに注意したい。実際、特徴量マップは複数の方法で用いることができる。特にクエリ複雑度などの下界値を議論する時には、特徴量マップ全体がアルゴリズムによって利用可能であることとしばしば仮定する。ローカルプランニングにおける上界値を議論する時には、プランナーが遭遇した状態の特徴量ベクトルをシミュレータから取得すると言うのが最も自然な仮定である。特にローカルプラニングを考えるときは、初期状態とともにその特徴量ベクトルが与えられ、また以降シミュレータを用いるたびに次の状態とともに対応する特徴量ベクトルが得られると言うのが自然な仮定である。

典型的なヒント

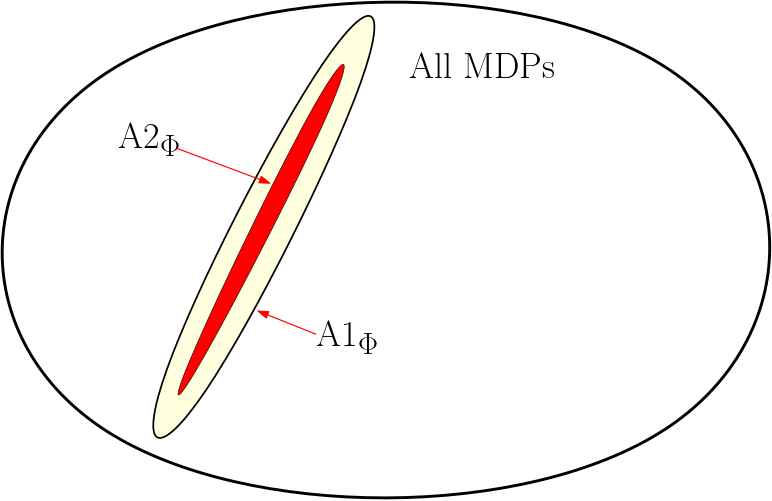
drawing

以降では、MDPと特徴量マップを紐付ける異なるヒント（仮定）のもとでのプランニングを考える。最も単純なものとして、 $\eqref{eq:vstr}$ が以下の仮定のもと成立する：

仮定 A1 ($v^*$ 実現可能性): MDP $M$ と特徴量マップ $\phi$ は $v^* \in \mathcal{F}_\phi$ を満たす。

2つ目のバリエーションは、全ての価値関数が表現可能な場合を考える：

仮定 A2 (普遍的価値関数実現可能性) MDP $M$ と特徴量マップ $\phi$ は全てのメモリーレス方策 $\pi$ において $v^\pi \in \mathcal{F}_\phi$ を満たす。

MDPの基本定理により $v^\pi = v^*$ となるメモリーレス方策 $\pi$ が存在するため、A2がA1を含むことは明らかである。上図は全てのMDPのうち、ある特徴量マップ $\phi$ (図中 A1$\mbox{}_\phi$）を用いる A1と、同じ特徴量マップを用いるA2（図中 A2$\mbox{}_\phi$）が占める部分を示す。両方とも全てのMDPのうち極めて小さい部分を占めているが、特徴量マップを変更すると、これらの和集合は明らかに全てのMDPを網羅する。そのようなヒントは一般的なものである。

これらの仮定には多くのバリエーションがある。しばしば、価値関数が正確に実現可能であるという仮定を緩和することが有用であることが分かる。そのように修正された仮定の下では、価値関数は特徴量マップの張る部分空間に含まれる必要はなく、その近辺にあればよい。使用されるべき自然な誤差指標は最大ノルムであり、その理由は後で明らかになる。これらの仮定をコンパクトに記述するため、 $v\in_{\varepsilon} \mathcal{F}$

の表記方法を導入し、以下を満たす：

\[\inf_{f\in \mathcal{F}} \| f - v \|_\infty \le \epsilon\,.\]

つまり、$v\in_{\varepsilon} \mathcal{F}$ は、 $\mathcal{F}$ からの $v$ への最良の近似値が一様に誤差 $\varepsilon$ が近似することを意味する。

上の $\varepsilon\ge 0$ を修正し $\in$ を $\in_{\varepsilon}$ に交換することで以下の仮定を得る：

仮定 A1$\mbox{}_{\varepsilon}$ (近似 $v^*$ 実現可能性): MDP $M$ と特徴量 $\phi$ は $v^* \in_{\varepsilon} \mathcal{F}_\phi$ を満たす。

仮定 A2$\mbox{}_{\varepsilon}$ (近似普遍的価値関数実現可能性) MDP $M$ と特徴量マップ $\phi$ は全てのメモリーレス方策 $\pi$ において $v^\pi \in_{\varepsilon} \mathcal{F}_\phi$ を満たす。

行動価値関数に関するヒント

状態行動対をベクトルに写像する特徴量関数を考える。具体的には、（表記を乱用して） $\phi: \mathcal{S}\times\mathcal{A}\to \mathbb{R}^d$ とすると A1 のように次の仮定を得る：

仮定 B1 ($q^*$ 実現可能性)：MDP $M$ と特徴量マップ $\phi$ は $q^* \in \mathcal{F}_\phi$ である。

ここで、 $\mathcal{F}_\phi$ は特徴量マップの範囲内にある関数の集合として定義される。また、同様にA2のように：

仮定 B2 (普遍行動価値関数実現可能性) MDP $M$ と特徴量マップ $\phi$ は任意のメモリーレス方策 $\pi$ において $q^\pi \in \mathcal{F}_\phi$ である。

また、正の近似誤差 $\varepsilon>0$ を導入することで B1$_{\varepsilon}$ と B2$_{\varepsilon}$ を得る：

仮定 B1$\mbox{}_{\varepsilon}$ (近似 $q^*$ 実現可能性): MDP $M$ と特徴量マップ $\phi$ は $q^* \in_{\varepsilon} \mathcal{F}_\phi$ である。

仮定 B2$\mbox{}_{\varepsilon}$ (近似普遍行動価値関数実現可能性) MDP $M$ と特徴量マップ $\phi$ は任意のメモリーレス方策 $\pi$ において $q^\pi \in_{\varepsilon} \mathcal{F}_\phi$ である。

なぜこれらの仮定のうちの1つを選ばないのかと思うかもしれない。ある仮定が別の仮定を暗示している場合、明らかに弱い仮定を選択することが好ましい。しかし、いくつかのケースでは強い仮定を用いることに価値がある場合や、仮定自体を簡単には比較できないこともある。

ノート

起源

価値関数近似をプランニングに使うというアイデアは少なくとも1960年代に端を発する。本講義末尾に初期の興味深い文献をいくつか示す。コンピュータがほとんど存在しておらず、計算能力が低かった時代にこのようなアイディアが既に登場していたというのは非常に興味深いことである。

無限空間

関数近似は状態または行動空間、またはその両方が「連続」（つまり、それらがユークリッド空間の部分集合）であるときに特に魅力的な方法である。このような場合、圧縮率は「無限大」となる。実験結果によると、MDPのプランニングでは関数近似は驚くほど多くのシナリオにおいてよく機能することが分かっている。空間が無限大の場合でも、全ての「計算」は成立するが、少し注意が必要な場合がある。例えば、$\Phi$ は行列であると明確に言うことはできないが、$\Phi$は、$\mathbb{R}^d$ を（特徴量マップが状態空間上のものである場合）状態空間上のすべての実数関数のベクトル空間に写像する線形演算子として明確に定義できる。

非線形価値関数近似

価値関数を圧縮するアイデアの最も成功した例がニューラルネットワークを使用したものである。読者はニューラルネットワークの基礎となる考え方は既にご存知であろう。ここでは、MDPプランニングにおいて線形関数近似の例で得られた知見が非線形関数近似の使い方にも影響を与えることを期待する。ある意味、最初の質問はプランニングアルゴリズムと関数近似技術のどれを用いるかを分離できるかどうかである。この問に対して、任意の特徴量マップを使えるかどうかについて考える。もし特徴量マップに関係なく性能を発揮するプランナーを見つけることができれば、特徴量マップとプランナーの性能を分離して考えることに成功し、特徴量マップの構成を非線形関数近似に一般化することを期待できる。しかしながら、もしうまく動作するプランナーが特徴マップの複雑な特性を利用する必要が有るとわかった場合、非線形関数近似に一般化した場合に複雑な問題が発生する可能性があることを警戒していると考えなければならない。いずれにせよ、まずはより簡単で分かりやすい線形の場合を検討することが賢明な戦略であると思われる。

アドバイス付き計算 / 不均一な計算（Computation with advice/Non-uniform Computation）

アドバイス付き計算とは、計算科学における一般的なアプローチの一つであり、ある写像を計算する問題を、アドバイスという追加の入力を持った写像を計算する問題に変更したものである。明らかに、ここでのアプローチはアドバイス付き計算の特殊なケースと見なすことができる。また、密接に関係する概念として、計算可能性・計算複雑度の分野で研究されてきた不均一な計算という概念がある。不均一な計算では、チューリングマシンは入力に加えて何らかの「アドバイス」の文字列を受け取る。

References

Richard Bellman, Robert Kalaba and Bella Kotkin. 1963. Polynomial Approximation–A New Computational Technique in Dynamic Programming: Allocation Processes. Mathematics of Computation, 17 (82): 155-161
Daniel, James W. 1976. “Splines and Efficiency in Dynamic Programming.” Journal of Mathematical Analysis and Applications 54 (2): 402–7.
Schweitzer, Paul J., and Abraham Seidmann. 1985. “Generalized Polynomial Approximations in Markovian Decision Processes.” Journal of Mathematical Analysis and Applications 110 (2): 568–82.
Brattka, Vasco, and Arno Pauly. 2010. Computation with Advice. arXiv [cs.LO].