6. ローカルプランニング - Part II.
前回の講義でローカルプランニングを導入した。 ローカルプランニングにおける重要なアイデアは、すべての状態に対し近似最適行動を出力させるのではなく、特定の状態に対してのみ行動を出力させることで、プランニングの計算コストを節約している点だ。そして、訪れる各状態でプランナーを呼び出し行動を生成することで誘導された方策が近似最適であるようにする。 この方法により、少なくとも決定論的MDPにおいては、プランニングのコストが状態空間の大きさに依存しないことを示した。 この方法を実現するために、価値反復の再帰的な実装を用いることが出来る。 その実装を簡単に説明するため、行動価値関数とそれに対応するベルマン最適作用素 ($T$) を次のように定義した:
\[\begin{align*} T q(s,a) = r_a(s) + \gamma \langle P_a(s), M q \rangle \end{align*}\](前回の講義では、この作用素を $\tilde T$ を用いて記述したが、見やすくするためにチルダを省く。)
また、実行時間 (またはクエリコスト) の面において、この単純な再帰的実装のよりも有意によいアルゴリズムが存在しないことを示した。 この講義では、このアイデアが確率的MDPの場合に拡張できることを示す。
サンプリングが身を助く?
MDPが確率的だとしよう。前回の講義で紹介した、$(T^k \boldsymbol{0})(s,\cdot)$ を計算するための再帰的価値反復の擬似コードを思い出そう:
1. define q(k,s):
2. if k = 0 return 0 # base case
3. return [ r(s,a) + gamma * sum( [P(s,a,s') * max(q(k-1,s')) for s' in S] ) for a in A ]
4. end
明らかに状態空間の大きさがline 3にこっそりと紛れ込んでいる。なぜなら、line 3において、$(s, a)$ の次状態分布に関する期待 値を計算しなければならないからだ。前述のように、決定論的システムにおいてシミュレータが使用できる場合、 可能な次状態上の総和が一度のシミュレータの実効で置き換えられる。 一方、期待値がサンプリングで近似出来ることを確率論入門の講義で学んだ読者も居るかもしれない。しかも、期待値計算には集合上での総和が必要となるが、その集合の要素数と近似誤差は独立であった。今考えているケースにおいて、その集合とは行動空間 $\mathcal{S}$ である。これは非常に幸運だ!
この近似誤差の大きさを計算するために、Hoeffdingの不等式を思い出そう:
補題 (Hoeffdingの不等式): 区間 $[0,1]$ に値をとる $m$ 個の独立同分布 (i.i.d.) 確率変数が与えられたとき、任意の \(0 \leq \zeta < 1\) に対し、確率 \(1 - \zeta\) 以上で次の不等式が成り立つ:
\[\left| \frac{1}{m} \sum_{i=1}^m X_i - \mathbb{E}[X_1] \right| \leq \sqrt{\frac{\log \frac{2}{\zeta}}{2m} }\]ある状態行動対 $(s,a)$ に対し、 $S_1’,\dots,S_m’ \stackrel{\textrm{i.i.d.}}{\sim} P_a(s)$ と $v:S \to [0,v_{\max}]$ を考えよう。この結果から、任意の $0\le \zeta <1$ に対し、確率 $1-\zeta$ で
\[\begin{align} \left|\frac1m \sum_{i=1}^m v(S_i') - \langle P_a(s), v \rangle\right| \le v_{\max} \sqrt{\frac{\log \frac{2}{\zeta}}{2m} } \label{eq:hoeffbop} \end{align}\]となる。
これは、次のような実装が可能であることを示唆する:各状態行動対 $(s,a)$ に対し、 $S_1’,\dots,S_m’ \stackrel{\textrm{i.i.d.}}{\sim} P_a(s)$ をサンプルし、リスト $C(s,a)$ に保存する。1 そして、ある関数 $v$ に対し $\langle P_a(s), v \rangle$ を計算する必要があるときには、サンプル平均
\[\frac1m \sum_{s'\in C(s,a)} v(s')\]を用いる。
この近似方法を以前の擬似コードに用いると、次の新たなコードを得る:
1. define q(k,s):
2. if k = 0 return 0 # base case
3. return [ r(s,a) + gamma/m * sum( [max(q(k-1,s')) for s' in C(s,a)] ) for a in A ]
4. end
このコードの総実行時間は $O( (m\mathrm{A})^{k+1} )$ となる。ここで重要なのは、方策の近似最適性の要求を満たしすような $m$ を $\mathrm{S}$ と独立に選べるならば、計算時間は状態空間の大きさとは独立に選べるということだ。
この擬似コードは、だれがいつリスト $C(s,a)$ を生成するのかという点をこっそりと無視している。 簡単で効果的なアプローチは”遅延評価” (または メモ化)だ: 初めて $C(s,a)$ が必要になったときそれを生成し、必要にならなければそもそも生成しない。 代わりとなる方法は、リストを保存せず、$(s,a)$ に対する次状態のサンプルが必要なときのみ生成する方法だ。両方とも有効な方法だが、リストを一度だけ作るというアプローチを考え、もう一方のアプローチについてはノートとして末尾でコメントしよう。
よい行動価値関数の近似があれば充分
このアプローチの長所と短所を理解するための最初のステップとして、$\hat T: \mathbb{R}^{\mathcal{S}\times\mathcal{A}} \to \mathbb{R}^{\mathcal{S}\times\mathcal{A}}$ を以下のように定義する:
\[(\hat T q)(s,a) = r_a(s) + \frac{\gamma}{m} \sum_{s'\in C(s,a)} \max_{a'\in \mathcal{A}} q(s',a')\]状態 $s=s_0$ と共に実行されたとき、プランナーは以下の行動を計算する。
\[\begin{align*} A = \arg\max_{a\in \mathcal{A}} \underbrace{ (\hat T^H \boldsymbol{0})(s_0,a) }_{Q_H(s_0,a)}\,, \end{align*}\]このすばらしい簡潔さ!
それでは、このプランナーによる方策 $\hat \pi$ がよい方策かどうか考えよう。 以前、最適価値関数とそれを近似する関数の近似誤差を、近似関数に貪欲な方策の最適方策からの外れ具合と結びつける結果を示した。まず最初に、これに相当する補題を述べよう。そのために、行動価値関数で最適価値関数に相当するものが必要となる。
$\epsilon$-最適貪欲方策の最適方策からの外れ具合
まず
\[q^*(s,a) = r_a(s) + \gamma \langle P_a(s), v^* \rangle\]と定義する。この関数 $q^*$ を (考えているMDPの) 最適行動価値関数 と呼ぶ。 この関数が \(M q^* = v^*\) であり、 \(q^* = T q^*\) を満たすのは簡単に確認できる。 前述の補題を以下に示す。
補題 (方策誤差バウンド - I.): $\pi$ をメモリーレス方策とし、関数 $q:\mathcal{S}\times\mathcal{A} \to \mathbb{R}$ と $\epsilon\ge 0$ を考える。以下のことが成立する:
-
$\pi$ が次の意味で $\epsilon$-最適貪欲 だとする: \(\sum_a \pi(a\vert s) q^*(s,a) \ge v^*(s)-\epsilon\) が各状態 $s\in \mathcal{S}$ について成立する。すると $\pi$ は $\epsilon/(1-\gamma)$-最適となる。つまり \(v^\pi \ge v^* - \frac{\epsilon}{1-\gamma} \boldsymbol{1}\,.\)
-
もし $\pi$ が $q$ について貪欲ならば、$\pi$ は $2\epsilon$-貪欲最適となる。ただし、\(\epsilon= \|q-q^*\|_\infty\) である。つまり
証明の一部は読者に委ねる。証明に便利ないくつかの記法を導入しよう。 特に、メモリーレス方策に対し、作用素 $M_\pi: \mathbb{R}^{\mathcal{S}\times \mathcal{A}} \to \mathbb{R}^{\mathcal{S}}$ を次のように定義する:
\[(M_\pi q)(s) = \sum_{a\in \mathcal{A}} \pi(a|s) q(s,a)\,, \qquad (q\in \mathbb{R}^{\mathcal{S}\times \mathcal{A}}, \, \, s\in \mathcal{S}).\]この作用素を用いて、$\pi$ の $q$ に関する貪欲性条件を
\[M_\pi q = M q\]と書ける。さらに、補題の最初の命題はより簡潔に $M_\pi q^* \ge v^* - 2\epsilon\boldsymbol{1}$ と書くことが出来る。
後ほど用いるので、$P_\pi: \mathbb{R}^{\mathcal{S}\times \mathcal{A}} \to \mathbb{R}^{\mathcal{S}\times \mathcal{A}}$ を次のように定義する:
\[P_\pi = P M_\pi\,.\]ここで、記法を乱用していることに注意しておく。なぜなら、$P_\pi$ はすでに、状態の関数を状態の関数に写す作用素として定義したからだ。しかし、$P_\pi$ の意味は文脈から明らかとなる。
証明: 最初の命題の証明は基本的なので、読者に委ねる。 二つ目の命題を証明するため、次のことに注意する。
\[\begin{align*} M_\pi q^* & \ge M_\pi(q-\epsilon \boldsymbol{1}) = M_\pi q - \epsilon\boldsymbol{1}=M q - \epsilon \boldsymbol{1} \ge M(q^* - \epsilon \boldsymbol{1}) - \epsilon \boldsymbol{1} = M q^* - 2\epsilon \boldsymbol{1} = v^* - 2\epsilon\boldsymbol{1}\,. \end{align*}\]これに最初の命題を適用することで証明が出来た。 \(\qquad \blacksquare\)
概$\epsilon$-最適貪欲方策の準最適性
ここで二つの問題がある。一つ目は、プランナーが $Q_H(s_0,\cdot)$ の計算を確率的に行っている点だ。そのため、シミュレータが出力したランダムな次状態が “代表的” でない可能性がある。そのような確率的計算の結果が常に正しいとは期待できない。 実際、私たちが期待できるのは、ある程度の確率で—出来れば1に近い確率で—結果が「正確」であることだ。Hoeffdingの不等式から、目標の確率以上で小さい誤差を達成するためには、サンプルサイズを増やす必要がある。しかしHoeffdingの不等式は、どうしても、失敗事象 が発生したときの誤差をコントロール出来ない。
結局のところ私たちが期待できるのは、”失敗事象” が発生した場合 (その発生確率をコントロールすることは後ほど考える) を除き、プランナーの各実行において、$Q_H(s_0,\cdot)$ が \(q^*(s_0,\cdot)\) に充分近いことだ。 この失敗確率を最大で $\zeta$ に抑えたいとしよう。このとき、この失敗事象を除き、誤差
\[\begin{align} \delta_H = \| Q_H(s_0,\cdot) - q^*(s_0,\cdot)\|_\infty \label{eq:d0def} \end{align}\]が小さくなって欲しい。 すると、上記の補題の証明の第一段階と同様に、この失敗事象を除き、プランナーが返す行動 $A$ が状態 $s_0$ において $2\epsilon$-最適貪欲
\[q^*(s_0, A) \ge v^*(s_0) - 2\epsilon\]と示すことが出来る。
プランナーが返した行動 $A$ が $a$ である確率を $\hat \pi(a \vert s_0)$ とする。つまり \(\hat \pi(a \vert s_0)=\mathbb{P}_{s_0}(A=a)\) となる。 ここで、$\mathbb{P}_{s_0}$ はプランナーとMDPシミュレータの相互作用によって誘導された確率測度だ。 すると、
\[\sum_{a} \hat \pi(a \vert s_0) \mathbb{I}( q^*(s_0, a) \ge v^*(s_0) - 2\epsilon ) = \mathbb{P}_{s_0}( q^*(s_0, A) \ge v^*(s_0) - 2\epsilon ) \ge 1-\zeta\,.\]言い換えると、少なくとも確率 $1-\zeta$ で、$\hat \pi$ は $2\epsilon$-最適貪欲行動を選択する。 これを 概$2\epsilon$-最適貪欲 であるという。 これは、$2\epsilon$-最適貪欲行動が常に選ばれるというケースほどよくはないが、$\zeta$ が $0$ に近づくにつれ、$\hat \pi$ と常に $2\epsilon$-最適貪欲行動を選ぶ方策のパフォーマンスの差は消えていくと考えられる。 なぜなら、パフォーマンスは行動確率に対し 連続的に 変化すると期待されるからだ。 以下の補題はこれを厳密に示している。
補題 (方策誤差バウンド II): $\zeta\in [0,1]$ とし、$\pi$ を、各状態で少なくとも確率 $1-\zeta$ で $\epsilon$-最適貪欲行動を選ぶ方策とする。このとき、次の不等式が成り立つ。
\[v^\pi \ge v^* - \frac{\epsilon+2\zeta \|q^*\|_\infty}{1-\gamma} \boldsymbol{1}\,.\]Proof: 以前の補題の最初の命題から、 $\pi$ が各状態で \(\epsilon+2\zeta \|q^*\|_\infty\)-最適貪欲だと示せばいいことが分かる。これは計算から示すことが出来るので、読者に任せる。 \(\qquad \blacksquare\)
誤差の抑制
最後に、式 \(\eqref{eq:d0def}\) で定義された誤差 $\delta_H$ が高い確率で小さくなることを証明する。 直感的には $\hat T \approx T$ となる。 これを示すために、式 \(\eqref{eq:hoeffbop}\) と集合 $\mathcal{C}(s,a)$ の選び方から、任意の固定された $(s,a)\in \mathcal{S}\times \mathcal{A}$ に対し、以下の式が少なくとも確率 $1-\zeta$ で成立することに注意する:
\[\begin{align} |\hat T q (s,a)-T q(s,a)| & = \gamma \left| \frac1m \sum_{s'\in \mathcal{C}(s,a)} v(s')\,\, - \langle P_a(s), v \rangle \right| \le \gamma \|q\|_\infty\, \sqrt{\frac{\log \frac{2}{\zeta}}{2m} } \nonumber \\ &\le \frac{\gamma}{1-\gamma}\, \sqrt{\frac{\log \frac{2}{\zeta}}{2m} } =: \Delta(\zeta,m), \label{eq:basicerror} \end{align}\]ただしここで、 $q\in \mathbb{R}^{\mathcal{S}\times \mathcal{A}}$ は固定された任意の$\mathcal{S}\times \mathcal{A}$上関数で $|q|_\infty \le \frac{1}{1-\gamma}$ を満たすものとし、$v = Mq$ と表記した。
ユニオンバウンド (ブールの不等式)
よって、任意の固定された状態行動対 $(s,a)$ に対し、低確率事象を除き、 $(\hat T q)(s,a)$ は $( T q)(s,a)$ に近くなる。しかし、 なんらかの 低確率事象を除き、 $(\hat T q)(s,a)$ が一様に $( T q)(s,a)$ へ近くなると結論付けることは出来るのだろうか?
これに答えるためには、逆に考えて、低確率な事象にも関わらず、この事象が起きなかった場合には、 $(s,a)$ に依存せず $(\hat T q)(s,a)$ が $( T q)(s,a)$ に近くなる事象を見つけるほうが簡単となる。
$\mathcal{E}(s,a)$ を $(\hat T q)(s,a)$ が $( T q)(s,a)$ から遠いという事象とする。つまり
\[\mathcal{E}(s,a) = \{ |(\hat T q)(s,a) - (\hat T q)(s,a)|> \Delta(\zeta,m) \}\]このとき、 $\mathcal{E} = \cup_{(s,a)} \mathcal{E}(s,a)$ とすると、$\mathcal{E}$ が起きなかった場合には、どの $\mathcal{E}(s,a)$ も起きていないと言えることは明らかだ。よって
\[\max_{(s,a)\in \mathcal{S}\times \mathcal{A}} |(\hat T q)(s,a) - (\hat T q)(s,a)|\le \Delta(\zeta,m)\]では $\mathcal{E}$ の確率はどれくらいになるのだろうか? これには、次の基本的な結果を用いることが出来る。この結果は測度の基本的性質から導かれる:
Lemma (ユニオンバウンド): 任意の確率測度 $\mathbb{P}$ と事象の加算列 \(A_1, A_2, \ldots\) に対し
\[\mathbb{P}\left(\cup_i A_i \right) \leq \sum_i \mathbb{P}(A_i)\]が成立する。
この結果から、$\mathcal{S}\times \mathcal{A}$ が加算であることを用いて、
\[\mathbb{P}(\mathcal{E}) \le \sum_{(s,a)\in \mathcal{S}\times \mathcal{A}} \mathbb{P}( \mathcal{E}(s,a)) \le \mathrm{S} \mathrm{A} \zeta\]が導かれる。もしこの確率を $0\le \zeta’\le 1$ としたいなら、$\zeta = \frac{\zeta’}{\mathrm{S}\mathrm{A}}$ とすることで、少なくとも確率 $1-\zeta’$ で任意の状態行動対 $(s,a)\in \mathcal{S}\times \mathcal{A}$ に対し、
\[\begin{align} |(\hat T q)(s,a) - (\hat T q)(s,a)| \le \Delta\left(\frac{\zeta'}{\mathrm{S}\mathrm{A}},m\right) = \frac{\gamma}{1-\gamma} \, \sqrt{\frac{\log \frac{2\mathrm{S}\mathrm{A}}{\zeta}}{2m} }\ \label{eq:ropec} \end{align}\]と結論出来る。以下の図はユニオンバウンドのアイデアをまとめたものである:
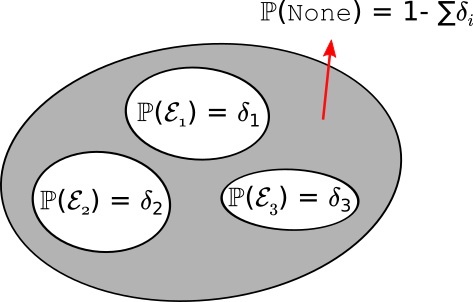
なんらかの不都合な事象が起きる確率を制御するためには、その事象を多数の基本的な部分に分割する。 そして、各基本的事象の確率を制御することで、もとの不都合な事象、または、余事象の”都合のいい”事象の確率を制御することが出来る。不都合な事象が起きる確率を制御するにあたり最悪のケースは、基本的事象たちが互いに素である場合だ。しかし、上記の議論はもちろんその場合も適用可能である。
もとの計算に戻ろう。最後の公式から、式 \(\eqref{eq:basicerror}\) に比べて誤差が増えることが分かった。しかし、増加量はあまり大きくない。 なぜなら、誤差は状態行動対数の対数に依存しているからだ。 対数的な誤差増加は大したことはないが、状態数が現れていることは残念だ。誤差を抑えるためには、この結果から、$m$ を状態数の対数に比例するように選ばなければならない。線形的な依存性に比べればマシだが、それでも依存は残ってしまう。 この依存性が本当に必要なのか疑問に思うかもしれない。 もしそうなら、決定論的MDPと確率的MDPでのプランニングには大きなギャップが存在することになる。 だが、ここで諦めるべきではない!
状態空間の濃度への依存の回避
状態の濃度に対する依存を避けるための鍵は状態行動集合全体におけるユニオンバウンドを取ることを避けることである. これが実現可能として良い理由は次の通りである. プランナーの再起的な実装を振り返ると, プランナーは全ての集合$\mathcal{C}(s,a)$に必ずしも依存していないことに気づくことができる.
これを処理するために, 集合$\mathcal{C}(s):=\cup_{a\in \mathcal{A}}\mathcal{C}(s,a)$によって挿入される状態間の距離を導入することが有用である. この状態$s$と$s’$の間の距離($\text{dist}(s,s’)$で表記される)は$s$から$s’$に到達するのに必要なステップ数の最小値を意味する. ここでは状態$s$から始まり, 各ステップで最終の状態に最も”近い”状態の一つを選べることを仮定している.
形式的には, $s_0=s$, $s_n = s’$である最短の長さ$n$の系列$s_0,s_1,\dots,s_n$のことである. ここで各$i\in [n]$について$s_i \in \mathcal{C}(s_{i-1})$が成り立つ. (これは$\mathcal{C}$によってエッジが挿入される状態に関する有向グラフ内における状態間の距離に該当する)
これを用いて, 全ての$h\ge 0$で状態$s_0$から高々$h$stepで到達可能な状態の集合を以下に定義する
\[\begin{align*} \mathcal{S}_h &= \{s \in \mathcal{S} | \text{ dist}(s_0,s) \leq h \} \end{align*}\]これはネストされた集合の系列であり, $\mathcal{S}_0 = {s_0}$, $\mathcal{S}_1$は$s_0$とその直近の”近傍”を含み以下同じような関係性が続くことを記載しておく.
関数$Q_H(s_0,\cdot)$の計算において関数$q$は$0\le k \le H$のある値を引数として呼び出される場合に, 呼び出し内で現れる全ての状態について\(s\in \mathcal{S}_{H-k}\)となることを今や観測してよい. これは$k=H$で始まる$k$に対する帰納法で証明できる.
証明を確認する.
基礎ステップは$q$が自身を呼び出すときは$k$が減少するためこれに従う. 従って$q$が$k=H$かつ状態$s$で呼び出された場合, $s=s_0$は真である. ゆえに$s\in \mathcal{S}_0$. 次に命題が$k=i+1$かつ$0\le i<H$で満たされると仮定する. $k=i$の時に$q$が呼び出す任意の状態$s'$をとってくる. $i<H$なので, これは再起的な呼び出しに違いない. (式3より)呼び出し連鎖をのぼっていくと, この再起呼び出しが実行された時点では, $k=i+1$である. (なぜなら再起呼び出し内では$k$の値はデクリメントされるから.) この呼び出しは(帰納法の仮定より)$s\in \mathcal{S}_{H-(i+1)}$を満たす状態$s$と行動$a\in \mathcal{A}$について$s'\in \mathcal{C}(s,a)$を満たす状態$s'$の全ての場合について呼び出される. $s$は$s_0$から高々$H-i-1$の距離にあり, 一方で$s$の”近傍"である$s’$は$s_0$から高々$H-i$の距離にある事になる. したがって$s\in \mathcal{S}_{H-i}$であり, 帰納法が成立する.集合 $\mathcal{C}(s,a)$ は使用されない $k=0$ で $q$ が呼び出される場合を考慮する(式2)と, $\mathcal{S}_{H-1}$ からの状態 $s$ のみが計算で集合 $\mathcal{C}(s,a)$ を使用するとわかる. したがって $|\mathcal{C}(s,a)|=m$ であるから,
\[\mathcal{S}_h \le 1 + (mA) + \dots + (mA)^h \le (mA)^{h+1}\,.\]そして特に, $\mathcal{S}_{H-1}\le (mA)^H$であり, これは状態空間のサイズに依存しない. もちろん初めからこれはよくわかっていた. こういうわけで合計の実行時間は状態空間の大きさとは独立している.
この利点を取り入れる方法は可能な状態行動対におけるユニオンバウンドを避けることである. 誤差に対する再起的な表現から始める.
$\delta_H = | (\hat T^H \boldsymbol{0})(s_0,\cdot)-q^*(s_0,\cdot)|_\infty$ が成立することを思い出そう. 三角不等式より,
\[\begin{align*} \delta_H & = \| (\hat T^H \boldsymbol{0})(s_0,\cdot)-q^*(s_0,\cdot)\|_\infty \\ &\le \| (\hat T \hat T^{H-1} \boldsymbol{0})(s_0,\cdot)- \hat T q^*(s_0,\cdot)\|_\infty + \| \hat T q^*(s_0,\cdot)- q^*(s_0,\cdot)\|_\infty\,. \end{align*}\]続いて以下のことを確認すると,
\[\vert \hat T q (s,a)-\hat T q^* (s,a) \vert \le \frac{\gamma}{m} \sum_{s'\in \mathcal{C}(s,a)} \vert Mq - v^* \vert (s') \le \gamma \max_{s'\in \mathcal{C}(s)} \vert Mq - v^* \vert (s')\,,\]以下の式がわかる.
\[\begin{align*} \delta_H \le \gamma \max_{s' \in \mathcal{C}(s_0), a \in \mathcal{A}} | (\hat T^{H-1} \boldsymbol{0})(s',a) - q^*(s',a) | + \| \hat T q^*(s_0,\cdot) - q^*(s_0,\cdot)\|_\infty \end{align*}\]特に, 以下の式を定義すると,
\[\delta_{h} = \underbrace{\max_{s'\in \mathcal{S}_{H-h},a\in \mathcal{A}} | \hat T^{h} \boldsymbol{0}(s',a)-q^*(s',a)|}_{=:\| \hat T^h \boldsymbol{0}-q^*\|_{\mathcal{S}_{H-h}}}\,,\]次の式に変形できる.
\[\delta_H \le \gamma \delta_{H-1} + \| \hat T q^* - q^* \|_{\mathcal{S}_0}\,,\]ここで以下の表記を活用する. $| q |_{\mathcal{U}} = \max_{s\in \mathcal{U},\max_{a\in \mathcal{A}}} |q(s,a)|$.
より一般的には$1\le h \le H$上で$h=H$から始める形で誘導することで次のように証明できる.
一方で,
\[\delta_0 = \| q^*\|_{\mathcal{S}_{H}} \le \| q^* \|_\infty \le \frac{1}{1-\gamma}\,,\]ここでは最後の不等式は単純化のために$r_a(s)\in [0,1]$を用いている. この$(\delta_h)_h$に対する再帰を展開するために, 以下の式を確認しよう.
\[\begin{align} \delta_H &\leq \frac{\gamma^H + \varepsilon'(1 + \gamma + \cdots + \gamma^{H-1})}{1 - \gamma} \leq \left(\gamma^H + \frac{\varepsilon'}{1 - \gamma} \right) \frac{1}{1 - \gamma} \label{eq:delta_H}. \end{align}\]右辺における足し算の中の第一項は$H$によって制御される. $\varepsilon’$は制御可能であることを示すことが残っている.($m$を適切に選ぶことで行われる.)
実際に$\varepsilon’$は\(q^* = T q^*\)を\(\hat T q^*\)で近似する際の最大ノルム誤差であるが,\(\mathcal{S}_{H-1}\)内の全ての状態においてのみこの誤差を制御する必要があることを述べておく. より最初の方に行った主張より, この集合は高々\((mA)^H\)の状態をもち, したがってこの誤差は$m$が状態数とは独立して選択される場合でさえ制御可能であることは妥当である.
\(\| \hat T q^* - q^* \|_{\mathcal{S}_{H-1}}\)の制御
\(\mathcal{S}_{H-1}\)は$(mA)^H$のみの状態を持つので, 思いつくこととしてはこの集合内の各状態の誤差に対するユニオンバウンドをとることがある. \(\mathcal{S}_{H-1}\)自体がランダムであることが問題である. そのようなものとして, 明白ではないが, 失敗事例はどのようなものなのだろうか?そして失敗事例はどの程度あるのだろうか?この集合のサイズもまだランダムである. 仮に\((A_i)_{i\in [n]}\)が各要素が\(\mathbb{P}(A_i)\le \delta\)でかつ \(I_1,\dots,I_k\in [n]\)のランダムな配列であると仮定すると, この$n$個の要素集合について任意の$k$個の事象のいずれかが発生する確率を \(\mathbb{P}( \cup_{j=1}^k A_{I_j}) \le k \delta\)で抑えることはできない. すなわちランダムに選択された事象に対するユニオンバウンドを適応することはできない. とりわけ, 最悪ケースでは発生確率は\(\mathbb{P}( \cup_{j=1}^k A_{I_j}) = n \delta\)になる.
\(\mathcal{S}_{H-1}\)が小さい集合であることを活用するために, もう一度集合の構造を活用する必要がある. \(\mathcal{S}_{H-1}\)のランダム性がそこまで問題にならない理由はこの集合を構築する特殊な方法にある. 最初に, 明らかに\(s_0\in \mathcal{S}_{H-1}\)は常に成立し, この状態では誤差\(\|(\hat T q^*)(s_0,\cdot)- Tq^*(s_0,\cdot)\|_\infty\)はヘフディングの不等式により制御可能である. 続いて, \(s_0\)の近傍を考える. もしも\(S\in \mathcal{C}(s_0)\)とすると, \(S=s_0\) で\(S\)における誤差が制御可能であることを既に知っている場合に該当するか, あるいは\(S\)が”真の近傍”であり, $q$の呼び出しに含まれる\(\mathcal{C}(S,a)\)の直ぐ内側(おそらく再帰が一度だけ走った時に含まれる要素のこと)の要素を生成することを考えることができるかのどちらかである. 最終的に, そのような近傍における誤差は制御可能である, なぜなら定義より全ての集合\(\mathcal{C}(s,a)\)(ここで$(s,a)$はすべての可能な状態行動対をみていくとする.) は独立して選択されるからである.
これは$q$の再起的呼び出し内で\(\mathcal{S}_{H-1}\)に含まれる状態が出現した時系列順を考慮すべきであることを示唆する. この順序を$S_1,S_2,\dots,S_n$であり, $n = 1+(mA)+\dots+(mA)^{H-1}$, $S_1=s_0$, $S_2$は$q$が呼びだす2番目の状態(必然的に \(S_2\in \mathcal{S}(s_0)\)), \(S_3\)を同様に3番目の状態としよう. 状態がこの系列中に複数回再出現する可能性があることを述べておく. さらに,集合の構造より, \(\mathcal{S}_{H-1} = \{ S_1,\dots,S_n \}\)である. この系列の長さはランダムでないことも述べておく. すなわちこの長さは$q$が呼び出される回数とちょうど同じである, ランダムでないとはっきりとわかる.
\(\| \hat T q^* - q^* \|_{\mathcal{S}_{H-1}}=\| \hat T q^* - Tq^* \|_{\mathcal{S}_{H-1}}\) が制御可能であることは以下の定理から直接導かれる:
定理: 即時報酬が $[0,1]$ の区間に含まれるとする. 任意の $0\le \zeta \le 1$について確率$1-\mathrm{A}n\zeta$で以下のことが成立する. 任意の $1\le i \le n$において, \(\begin{align*} \| \hat T q^* (S_i, \cdot)- q^* (S_i,\cdot) \|_{\infty} \le \Delta(\zeta,m)\,, \end{align*}\) ここで \(\Delta\) は \(\eqref{eq:basicerror}\)により与えられる.
証明: 次のことを思い出そう. $\mathcal{C}(s,a) = (S_1’(s,a),\dots,S_m’(s,a))$とする. ここでは二つのことが成り立つ. (i) \((\mathcal{C}(s,a))_{(s,a)}\) が相互に独立しており, (ii) 任意の $(s,a)$について, $(S_i’(s,a))_i$ は共通の分布$P_a(s)$に従い i.i.d. を満たす系列である.
すべての $s\in \mathcal{S}$, $a\in \mathcal{A}$, $C\in \mathcal{S}^m$ について以下のようにする.
\[\begin{align*} g(s,a,C) = \left| \frac{\gamma}{m} \sum_{s'\in C} v^*(s') \,\, - \langle P_a(s), v^* \rangle \right| \end{align*}\](以前と同様に, $s’\in C$ は $s’$ が系列 $C$の内の要素を構成している集合の要素であることを意味する.) $\hat T$の定義と $q^*$の性質から以下のことが成立することを思い出そう. \(\begin{align} |\hat T q^*(s,a)- q^*(s,a)| = \left| \frac{\gamma}{m} \sum_{s'\in \mathcal{C}(s,a)} v^*(s') \,\, - \langle P_a(s), v^* \rangle \right| = g(s,a,\mathcal{C}(s,a)) \,. \label{eq:dub} \end{align}\)
$i$を\(1 \le i \le n\)で固定する. $\tau = \min{ 1\le j \le i\,:\, S_j = S_i }$としよう. すなわち, $\tau$ は$S_i$ が初めて系列 $ {S_i}_i$ に出現する時間である.
$a$を$a\in \mathcal{A}$で固定する. 与えられた $S_{\tau}$, $(S_j’(S_{\tau},a))_{j=1}^m$ は共通の分布 $ P_a(S_{\tau})$ について i.i.d.であることを述べておく.すなわち, 任意の $s, s_1’,\dots,s_m’\in \mathcal{S}$ について, \(\begin{align} \mathbb{P}( S_1'(S_{\tau},a)=s_1',\dots, S_m'(S_{\tau},a)=s_m' \, \vert\, S_{\tau}=s) = \prod_{j=1}^m P(s,a,s_j') \label{eq:indep} \end{align}\) これが与えられたことにより, 任意の $\Delta\ge 0$について, \(\eqref{eq:dub}\)より,
\[\begin{align*} \mathbb{P}( & |\hat T q^*(S_i,a)- q^*(S_i,a)| > \Delta ) = \mathbb{P}( g(S_i,a,\mathcal{C}(S_i,a)) > \Delta ) \\ & = \mathbb{P}( g(S_{\tau},a,\mathcal{C}(S_\tau,a)) > \Delta ) \\ & = \sum_{s} \mathbb{P}( g(s,a,\mathcal{C}(s,a)) > \Delta, S_{\tau}=s ) \\ & = \sum_{s} \sum_{1\le j \le i} \mathbb{P}( g(s,a,\mathcal{C}(s,a)) > \Delta, S_j=s, \tau=j ) \\ & = \sum_{s} \sum_{1\le j \le i} \sum_{\substack{s_{1:j-1} \in \mathcal{S}^{j-1}:\\ s\not\in s_{1:j-1}}} \mathbb{P}( g(s,a,\mathcal{C}(s,a)) > \Delta, S_j=s, S_{1:j-1}=s_{1:j-1})\\ & = \sum_{s} \sum_{1\le j \le i} \sum_{\substack{s_{1:j-1} \in \mathcal{S}^{j-1}:\\ s\not\in s_{1:j-1}}} \mathbb{P}( g(s,a,\mathcal{C}(s,a)) > \Delta, \phi_j( s,s_{1:j-1},\mathcal{C}(s_1),\dots,\mathcal{C}(s_{j-1}) )=1 )\,, \end{align*}\]なんらかのブール値関数 $\phi_1$, $\dots$, $\phi_i$を定義する. ここではすべての$j$($1\le j \le i$)について, $\phi_j$が
\[\phi_j( s,s_{1:j-1},\mathcal{C}(s_1),\dots,\mathcal{C}(s_{j-1}) )=1\]となることを$S_j=s, S_{1:j-1}=s_{1:j-1}$の時にのみ満たす. ただし, $s\in \mathcal{S}$ と $s_{1:j-1}\in \mathcal{S}^{j-1}$ は$s\not\in s_{1:j-1}$を満たす任意なものとする. そのような関数が存在することは $S_{1:j}=s_{1:j}$を任意の系列$s_{1:j}$について保証するには集合$\mathcal{C}(s_1),\dots,\mathcal{C}(s_{j-1})$の知識があれば十分であるということによる. すなわち, 近似関数は初めに$S_{1:j}=s_{1:j}$を確認して, $S_1=s_1$の時のみ, 次に$S_2=s_2$の確認に移るなどという形をとる.
前提より, すべての $s\not\in s_{1:j-1}$について$\mathcal{C}(s,a)$と$\phi_j( s,s_{1:j-1},\mathcal{C}(s_1),\dots,\mathcal{C}(s_{j-1}) )=1$ は互いに独立である. ゆえに,
\[\begin{align*} \mathbb{P}( & g(s,a,\mathcal{C}(s,a)) > \Delta, \phi_j( s,s_{1:j-1},\mathcal{C}(s_1),\dots,\mathcal{C}(s_{j-1}) )=1 )\\ & = \mathbb{P}( g(s,a,\mathcal{C}(s,a)) > \Delta) \cdot \mathbb{P}(\phi_j( s,s_{1:j-1},\mathcal{C}(s_1),\dots,\mathcal{C}(s_{j-1}) )=1 )\,. \end{align*}\]これを以前に表示した等式に接続すると, 全確率の法則を用いてなされた拡張を展開して, 次のようになる.
\[\begin{align*} \mathbb{P}( |\hat T q^*(S_i,a)- q^*(S_i,a)| > \Delta ) & = \sum_{s} \mathbb{P}( g(s,a,\mathcal{C}(s,a)) > \Delta ) \mathbb{P}( S_\tau = s )\,. \end{align*}\]今や, $|q^*|_\infty \le 1/(1-\gamma)$のため, 任意の固定された $(s,a)$について\(\mathbb{P}( g(s,a,\mathcal{C}(s,a)) > \Delta(\zeta,m) )\le \zeta\)となるように, $\Delta = \Delta(\zeta,m)$ を \(\eqref{eq:basicerror}\) から選択する. これを過去に表示したものに接続すると次の式を得る.
\[\begin{align*} \mathbb{P}( |\hat T q^*(S_i,a)- q^*(S_i,a)| > \Delta(\zeta,m) ) \le \zeta \sum_{s} \mathbb{P}( S_\tau = s ) = \zeta\,. \end{align*}\]この主張はすべての行動とすべての $1\le i \le n$に対するユニオンバウンドについて満たされる. \(\qquad \blacksquare\)
誤差バウンドまとめ
今までの導出をまとめると、任意の$0\le \zeta \le 1$について、プランナーによって得られる$\hat \pi$は
\[\epsilon(m,H,\zeta):=\frac{2}{(1-\gamma)^2} \left[\gamma^H + \frac{1}{1-\gamma} \sqrt{ \frac{\log\left(\frac{2n\mathrm{A}}{\zeta}\right)}{2m} } + \zeta \right]\,.\]なる$\epsilon(m,H,\zeta)$-最適である。 つまり、$\delta$-最適な方策を得るには、上式の3つの項がそれぞれ$\delta/3$になるように$H$、$\zeta$および$m$を調整すれば良い。
\[\begin{align*} \frac{2\gamma^H}{1-\gamma} & \le (1-\gamma)\frac{\delta}{3}\,,\\ \zeta & \le (1-\gamma)^2\frac{\delta}{6}\, \qquad \text{and}\\ \frac{m}{\log\left(\frac{2n\mathrm{A}}{\zeta}\right)} & \ge \frac{18}{\delta^2(1-\gamma)^6}\,. \end{align*}\]よって、 $H$は$H = \lceil H_{\gamma,(1-\gamma)\delta/6}\rceil$、$\zeta$は$\zeta = (1-\gamma)^2\delta/6$と設定すれば、 1つめと3つめの項は$\delta/3$以下になる。 さて、 最後の不等式を満たす最小の$m$を導出するため、 $n = (mA)^H$であることを思い出そう。 また、 $m$の導出には次の不等式を利用する (導出は省略):
命題: $a>0$、$b\in \mathbb{R}$、\(t^*=\frac{2}{a}\left[ \log\left(\frac1a\right)-b \right]\)とする。 この時、任意の正の実数$t\ge t^*$について、
\[\begin{align*} at+b > \log(t)\,. \end{align*}\]が成立する。
上の不等式を利用して、
\[c_\delta = \frac{18}{\delta^2(1-\gamma)^6}\]および
\[\begin{align} m^*(\delta,\mathrm{A}) = 2c_\delta \left[ H \log(c_\delta H) + \log\left(\frac{12}{(1-\gamma)^2\delta}\right) + (H+1) \log(\mathrm{A}) \right] \label{eq:mstar} \end{align}\]とすると、$m \ge m^*$の時、全ての不等式が成立する. 以上の結果を合わせて、次の結果を得る:
定理: 即時報酬は$[0,1]$の範囲で定義されているとする。 任意の$\delta\ge 0$と任意の割引率$\gamma$のMDPについて、$\delta$-最適な方策を、最大でも\(O( (m^* \mathrm{A})^H )\)の毎ステップの処理で獲得できるプランナーが存在する. ここで、$m^*(\delta,\mathrm{A})$は \(\eqref{eq:mstar}\) によって与えられ、また、 $H = \lceil H_{\gamma,(1-\gamma)\delta/3}\rceil$ である。
MDPが決定的な場合と比較すると、計算量が増大していることが分かる (対数項を無視すれば、上の結果では$m = H^8/\delta^2$だが、決定的な場合は$m=1$で済む!)が、最終的に得られた計算量は状態空間の大きさに依存しない。 しかし、最悪なケースではエフェクティブホライゾンが指数依存であることに注意してほしい。 次の章では、この指数的な計算量を回避できるようなプランナーについて考えていく。
Notes
疎な先読み木
この章で学んだアルゴリズムはKearns, Mansour and Ng from 2002の論文が元になっている。 この論文では、毎ステップで新しい集合$\mathcal{C}(s,a)$を生成する。 毎回$\mathcal{C}(s,a)$を生成する場合はBelmman作用素を近似していると考えるのが難しくなる(なんで?)が、全体的に見ればどちらのアルゴリズムもやっていることは一緒だ。 実際、$H$個のランダムな作用素: $\hat T_1$、$\dots$、$\hat T_H$ (上述した$\hat T$と同じだが$\hat T_h$は「プライベートな」集合$( \hat C_h(s,a) )_{(s,a)}$を保持している)を導入すると、Kearnsらのアルゴリズムは
\[A = \arg\max_{a} (\hat T_1 \dots \hat T_h \boldsymbol{0})(s_0,a)\]を計算しているとみなせる.
実は今回の内容に上の式を適用するのはそれほど難しくない。 この場合は、価値関数を「疎な先読み木」を$s_0$に何度も適用しているのと同じになるからだ。
今回学んだアイディアを元に、これまでに多くの研究が行われ, 最終的に様々なモンテカルロ木探索アルゴリズムが開発されてきた (例えばUCTなど. yours truly’sってなに?)。 一般に、これらのアルゴリズムは計算量を減らすために木を必要なときにだけ生成することが多い。結論から言えば、”根”での価値が高い確率で向上するようなノードを広げる戦略が効果的なのである (何この話?)。これは、「楽観的なプランニング」として知られている。例えばA* (また、そのMDP版であるA0)はこの楽観性に基づいている: Aで使用するヒューリスティック関数は最適価値の上界に相当する(なにこれ?)。 モンテカルロ木探索についての理論はRemi Munos’s monographを参考にして欲しい。
測度の集中現象
Hoeffdingの不等式は測度の集中現象(雑に言うとたくさんのパラメータに依存しているLipschitz連続な関数はほとんど定数になるっている話らしい?)の特別な場合である。これは、サンプルによって得られた測定値が全ての測度について(?)良い近似になることを意味している。 最もシンプルな例は平均値で (サンプルによって近似したもの)、平均の周りの集中不等式に繋がる。 Hoeffdingの不等式は集中不等式の一例である。 Hoeffdingの不等式の良いところ(シンプルさ以外で)は、失敗確率$\delta$ (後で$\zeta$とする)が対数の中に現れる点である。 つまり、より厳密にする場合にかかるコストが小さいのだ。 Hoeffdingの不等式のような依存性(つまり$\sqrt{ \log(1/\delta)})$)が現れる場合、sub-Gaussian型の偏差であるという(Gaussian型の確率変数はこのような不等式を満たすので)。 測度の集中現象と集中不等式は確率論の重要なトピックであり、多くの文献がこれについて言及している。 特に良さそうなものはこのNotesの最後に記載した。勉強する場合はPollardの短めの本やVershyninの本をおすすめする。
対数関数と線形関数の関係
対数関数と線形関数についての不等式はこのProposition 4を参照して欲しい. 証明で大事なことは次の2つだ: まず、$b=0$のときについてのみ考えれば十分である。そして、$a\ge 1$のとき、この結果は自明であり、$a< 1$のとき、$t\mapsto at$の増加率が$t\mapsto \log(t)$の増加率の二乗(?)に対応することに基づいている (ここの翻訳ムズ…証明を確認するべき)。
A model-centered view and random operators
本講義では、$\hat T$が$T$の良い近似であり、そのため、$T$の代わりに使用できることを学んだ。 これは$\hat T$で使用するデータがMDPの近似であることからも説明できる; MDPの確率的な近似において、その遷移確率は
\[\hat P(s,a,s') = \frac1m \sum_{s''\in C(s,a)} \mathbb{I}\{ s''=s'\}\]で定義される。 $C(s,a)$の要素数が少ないのに(つまり$m$がちいさいのに)次の状態の分布がよく近似できるのは奇跡的に見えるかもしれない。しかし、これがランダム性の便利なところなのだ! ランダムな作用素 (もしくは毎ステップで新しいランダムなサンプルを集めるような逐次的な作用素)を使用した動的計画法は経験的動的計画法Haskell et al.。
あるモデルが「真のMDP」の「良い」近似であるためには、そのモデルによるベルマン最適作用素が真のMDPのベルマン最適作用素に「近い」近似になることが重要なのだ
では、シミュレータが完璧ではない場合には何が起こるのだろうか?
シミュレータが完璧ではないときは?
完璧なシミュレータを想定できる状況は少ない. しかし、シミュレータが完璧でないときでも、だいたい同じことが成り立つ。 上述したように、シミュレータによって近似したベルマン最適作用素が、真のMDPのベルマン最適作用素に近い時、真のMDPでも良く動作する方策が期待できる。 実際、上述した証明はこのことを示すための要素を全て含んでいる。 特に、$\hat T$が$\gamma$ max-norm contraction (和訳思いつかない)であり、$\hat q^*$がその収束点である場合、
\[\|\hat q^* - q^*\|_\infty \le \frac{\| \hat T q^* - T q^* \|_\infty}{1-\gamma}\,,\]であり、本章の方策の誤差バウンドについての最初の補題によれば、$\hat q^*$ についての貪欲な方策は、$T$ についてのMDPで
\[\frac{2 \| \hat{T} q^* - T q^* \|_\infty}{(1-\gamma)^2}\]最適になる。
モンテカルロ法
Homework 0ではランダム化が少し便利であることを確認し、今回はランダム化がもっと役に立つことを確認した。 representation(和訳思いつかん)が大事なことを再確認して欲しい: もしMDPが”生成的なシミュレータ”とともに与えられていない時、そのようなシミュレータを得ることは本当に難しい。このことはモデルを学習する際に覚えておくと良い:
プランナーの仕事を楽にするようなモデルの学習にこだわるべきである.
生成モデルはそのようなモデルの1つであり、本章で見たように、状態数に関わる前回の下界と合わせて証明可能だ。 ランダム化は、より一般的にはコンピュータ・サイエンスの強力なツールであり、やや哲学的な疑問も含んでいる: ランダム性とは何だろうか? 「真のランダム性」は存在するのか?「真のランダム性」を利用できるコンピュータは作れるのだろうか?
真のランダム性?
「真の」ランダムせいとはなんだろうか? これを説明できるほどの余裕はだいたいない。なので、大体の場合はこの問題はそのまま放置される。しかし、この問題はコンピュータ・サイエンスの理論で徹底的に研究された問題であり、わかりやすい結果と本が出ている。 AroraとBarakの本の(第7章、20章および21章)は良いイントロダクションになるだろう。
集合$C(s,a)$は再利用していいのか?
シミュレーションが高コストである場合、プランナーの実行の際に集合を再利用したくなるかもしれない. 結局、集合を再利用しても、$\hat \pi$はどの状態でも高確率で$\epsilon$-最適化行動を選択するという性質を持つことになる。 しかし、これは良いアイデアではないかもしれない。何がいけないのか、読者に考えてもらいたいと思う。 この証明には、プランナーが呼び出しのたびに使う新しいランダム演算子$\hat T$を利用する。しかし、これはどこで使われるのだろう?
MDP文献における連続性議論の偏在性
MDPを使った計算はすべて近似的に行われる. 方策の評価は近似的に行われ、ベルマン作用素は近似的に計算される。我々は近似的なモデルを持ち、近似的な貪欲法を利用している. もしこれらの処理のどれかが小さな誤差を拡大するようなことがあれば、どの近似モデルも機能しなくなるだろう. 近似計算の研究は(大きなMDPに直面した場合には必ず必要になる)、得られる結果の導入された誤差に対する感度の研究である. これは数値解析の分野では誤差解析と呼ばれてる。他の数学の分野では感度分析と呼ばれている。実際、感度分析では、入力の変化に対しる出力の変化を確認するため、導関数を計算することがよくある (データが近似される)。何について微分すればいいのだろう? データが近似されるので、変化していくデータについて微分すれば良い。実際、微分に基づいた感度分析はどこでも使用できる。これは「古い」MDPの文献でも言及されており、方策勾配の定理にも関連している(これについては後ほど説明する)。古くから研究されてきたが、もしかしたらこのアプローチにはまだ見ぬ素晴らしい発見があるかもしれない。
References
- Kearns, M., Mansour, Y., & Ng, A. Y. (2002). A sparse sampling algorithm for near-optimal planning in large Markov decision processes. Machine learning, 49(2), 193-208. [link]
- David Pollard (2015). A few good inequalities. Chapter 2 of a book under preparation with working title “MiniEmpirical”. [link]
- Stephane Boucheron, Gabor Lugosi and Pascal Massart (2012). Concentration inequalities: A nonasymptotic theory of indepndence. Clarendon Press – Oxford. [link]
- Roman Vershynin (2018). High-Dimensional Probability: An Introduction with Applications in Data Science. [link]
- M. J. Wainwright (2019) High-dimensional statistics: A non-asymptotic viewpoint. Cambridge University Press.
- Lafferty J., Liu H., & Wasserman L. (2010). Concentration of Measure. [link]
- Lattimore, T., & Szepesvári, C. (2020). Bandit algorithms. Cambridge University Press.
- William B. Haskell, Rahul Jain, and Dileep Kalathil. Empirical dynamic programming. Mathematics of Operations Research, 2016.
- Sanjeev Arora and Boaz Barak (2009). Computational Complexity: A Modern Approach. Cambridge University Press.
- Remi Munos (2014). From Bandits to Monte-Carlo Tree Search: The Optimistic Principle Applied to Optimization and Planning. Foundations and Trends in Machine Learning: Vol. 7: No. 1, pp 1-129.
翻訳者注
-
おそらく、状態を$s$に固定したときの各状態行動対を意味している。つまり、$(s, a)_{a \in \mathcal{A}}$。 ↩