11. $v^*$実現可能性のもとでのプランニング (テンソルプラン I.)

前回の講義では、線形関数近似による$q^*$実現可能性のもとでは、アクションの数に制限を設けないと、固定ホライゾンでのローカルプランニング問題を、一定の準最適ギャップのもとで、クエリ効率よく解くことはできないということがわかった。特に、クエリ数の指数的な増大を示すために用いたMDP群では行動が$e^{\Theta(d)}$通りある。ただし、$d$ は最適状態行動価値関数を実現する特徴量マップの次元だ。講義の最後では、割引なし無限ホライゾンの問題についても、行動数が$d$に線形に増えるような場合は、線形関数近似による$v^*$実現可能性のもとで必要なクエリ数が指数的に増えることについて触れた。この講義では$v^*$実現可能性についてさらに吟味していくが、再び固定ホライゾン設定を用い、また行動数が固定な場合を考える。この設定では、後ほどわかるように、クエリ効率のよいプランニングが可能になる。

詳細な結果を与える前に、少し基礎固めをして、他の定義を見直しておこう。はじめに、ホライゾン$H$の設定で、特徴量マップ$\phi=(\phi_h)_{0\le h \le H-1}$のもとでの$v^*$-実現可能性は、以下を意味する。

\[\begin{align} \inf_{\theta\in \mathbb{R}^d} \max_{0\le h \le H-1}\|\Phi_h \theta - v^*_{h} \|_\infty = 0\,, \label{eq:vsrealizability} \end{align}\]

ただし、 $v^*_h$ は、残り $H-h$ ステップのときの最適価値関数だ (特に、$v^*_H=\boldsymbol{0}$)。ここでも、前回の講義で導入したインデックスづけを使用している。続く内容では、一般性を失うことなく、全ての特徴ベクトルが(ユークリッドノルムで)半径1のボールの中におさまるような特徴量マップを仮定する。ユークリッドノルムが$B$以内にバウンドされているようなある特徴量ベクトルのもとで、この実現可能性が成り立つとき、$v^*$が特徴量マップ$\phi$のもとで $B$実現可能であると呼ぶ。

下の図で示すように、我々はプランナ・シミュレータ間のインタラクションプロトコルに少し変更を加える。特に異なるのは、ステージが導入されていること、プランナのステージと特徴量へのアクセスがシミュレータのローカル呼び出しに制限されていることだ。

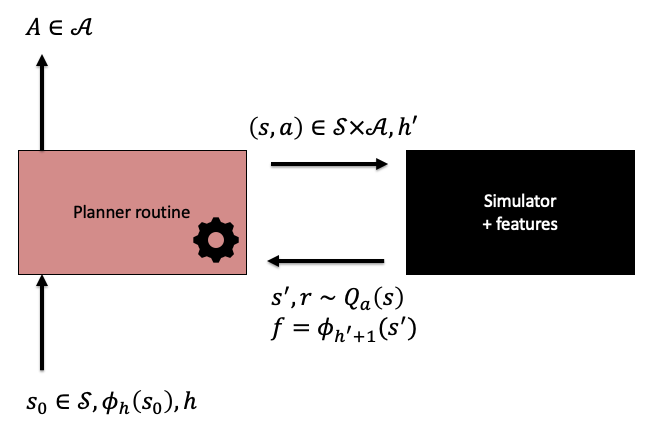
drawing
プランナ・シミュレータ間のインタラクションプロトコルを示すイラスト。

ホライゾン固定の問題ではステージのインデックスがとるべき行動に影響を与えるため、プランナは初期状態$s_0$とステージインデックス$h$で呼ばれる。プランナに基づく方策を定義するために、プランナが最初にある状態で、$h=0$で呼ばれることを仮定する。すると、プランナが行動を選択し、遷移した状態でプランナが$h=1$で呼ばれる、といった具合だ。シミュレータとインタラクションしている間、プランナはそれまで訪問した状態だけを使うよう制限される。また、プランナはシミュレータにステージインデックスを与え、そのインデックスに基づき、次のステージでの次状態での特徴量を得る。他の方法で特徴量にアクセスすることはできない。前回の講義と同様に、我々はMDPの報酬にランダム性を許す(確率変数とする)。

この設定での$\delta$-健全なプランナは、上記のプロトコルのもとで、使用するシミュレータが基づいているMDPにおいて$\delta$-準最適であるような方策を出す。

定理 ($v^*$-実現可能性のもとでのクエリ効率のいいプランニング): 任意の整数 $A,H>0$ と実数 $B,\delta>0$について、以下の性質を満たすローカルプランナー$\mathcal{P}$が存在する:

プランナー$\mathcal{P}$は、ホライゾン$H$のプランニング問題と、MDPと特徴量マップの組$(M,\phi)$のクラスで、$v^*$が$\phi$のもとで$B$-実現可能になり、$M$がたかだか$A$種類の行動しかもたず、また報酬が$[0,1]$の範囲にバウンドされるようなものについて、$\delta$-健全である。
各呼び出しにおいて、プランナによって使用されるクエリの数は、たかだか

\[\begin{align*} \text{poly}\left( \left(\frac{dH}{\delta}\right)^A, B \right) \end{align*}\]

固定された$A>0$ について、クエリコストが$d,H,1/\delta$ および $B$の多項式になることに注意しよう。このバウンドが改善できるかどうかはオープンプロブレムだ。 $v^*$実現可能性のもとでは、$v^*$を実現する$\theta\in \mathbb{R}^d$が知られていてもなお、これはどういうわけか理論上の研究課題になっている。しかし、追加の情報がないという設定のもとでは、$v^*$から行動価値関数$q^*$の良い近似を手に入れるために少なくとも$\Theta(A)$回はシミュレーションを呼び出す必要があり、これは良い方策を導くのに必要なコストに思える。よって、クエリコストは少なくとも$A$に線形にスケールする必要があり、行動の数が多すぎるとき、クエリ効率のいいアルゴリズムは存在しない。

TensorPlan: 楽観的なプランナ

先の定理で登場したプランナをTensorPlanと呼ぶ。この名前の由来は、アルゴリズムの説明をした後で明らかになるだろう。

TensorPlanは、楽観的なアルゴリズムのクラスに属している。 $v^*$を実現するパラメタベクトル$\theta^*$ がわかっているなら、準最適な行動をとるには十分なはずだ。そのため、このアルゴリズムは、そのようなパラメタベクトルの良い近似を見つけることを目指す。

これを満足する推定値は、以下の2ステップにより構成される。

アルゴリズムは、非空である「仮説」集合$\Theta\subset \mathbb{R}^d$を保持する。これは、アルゴリズムがそれまで観測したデータと整合性のとれるようなパラメタベクトルを含む。この集合の構成の詳細がアルゴリズムの核となるが、これは後ほどすぐ見ていくことにしよう。
与えられた$\Theta$について、以下の最大化問題を解くことにより推定値 $\theta^+$ を与える。

\[\begin{align} \theta^+=\arg\max_{\theta\in \Theta} \phi_0(s_0)^\top \theta\,. \label{eq:optplanning} \end{align}\]

ここで、$s_0$はエピソードの最初の状態であり、すなわち、これは$h=0$のときにプランナが呼ばれる状態である。 $\phi_0(s_0)^\top \theta^* = v_0^*(s_0)$であることを思い出すと、$\theta^*\in \Theta$のもとで、

\[v_0(s_0;\theta^+)\ge v_0^*(s_0)\,,\]

となることがわかる。ここで、簡便のため、$v_h(s;\theta) = \phi_h(s)^\top \theta$とした。 $\theta^+$が$\theta^*$に十分近づくとき、$\theta^+$に基づく方策が最適に近くなることが期待できそうだ。よって、ここでとるアプローチは、あるパラメタに基づく方策を用いて(シミュレータを使って)ロールアウトを行い、ロールアウトによって観測されるデータがベルマン方程式と整合性がとれているかどうかを確認することだ。結果的に、観測されたエピソードのリターンが$v_0(s_0;\theta^+)$に近いかどうかもチェックすることになる。もしこれらの条件との矛盾が見つかった場合、ロールアウトにより得られたデータは、(ベルマン方程式と)整合するパラメタべクトルの集合$\Theta$を縮小するために使える。

ここまで説明したアプローチでは、$\theta^+$に「基づく」方策が何を意味するかには触れていない。ナイーブな方法は、以下のベルマン最適方程式に基づいて方策を構成することだ。

\[\begin{align} v_h^*(s) = \max_a r_a(s)+ \langle P_a(s), v_{h+1}^* \rangle \label{eq:fhboe} \end{align}\]

これは$h=0,1,\dots,H-1$について成り立ち、$v_H^* = \boldsymbol{0}$となる。もし$\theta^+= \theta^*$ならば、$v_h(\cdot;\theta^+)$ もまたこの方程式を満たす。よって、$v_{h+1}^*$を$v_{h+1}(\cdot;\theta^+)$に置きかえれば、式\eqref{eq:fhboe}の右辺を最大化するような行動を選ぶ方策を定義できる。 $\theta^+$のベルマン方程式との整合性は、この方程式中の$v^*_{\cdot}(\cdot)$を$v_{\cdot}(\cdot;\theta^+)$により置きかえたとき、\eqref{eq:fhboe}が(近似的に)成り立つかどうかによっても確認できる。想像がつくかもしれないが、これはシミュレータからデータを生成することで確認できる。

この(ナイーブな)アプローチはうまくいきそうだが、それを確認するのは容易ではない (実際、これがうまくいくかどうかはオープンプロブレムだ!)。 TensorPlanは、$\theta^+$に基づく方策と整合性を少し違った形で定義する。変更された定義は、TensorPlanのクエリ効率がいいことを証明するためだけでなく、TensorPlanに、上の定理で言及したよりも強い保証を与える。

ベルマン最適方程式に基づくアルゴリズムの解析を難しくしているのは、この方程式において最大値をとっている部分だ。よって、TensorPlanはこの最大化を除去する。そして、$\theta^+$に基づく方策を、状態$s$とステージ$h$において、以下の等式を満たす任意の行動 $a\in \mathcal{A}$を選ぶ任意の方策$\pi_{\theta^+}$として定義する。

\[\begin{align} v_h(s;\theta^+) = r_a(s)+ \langle P_a(s), v_{h+1}(\cdot;\theta^+) \rangle\,. \label{eq:tpcons} \end{align}\]

これを満たす行動がない場合、 $\pi_{\theta}$はどんな行動を選んでもよい。我々は、式\eqref{eq:tpcons}を満たす行動$a\in \mathcal{A}$が存在するとき、$(s,h,\theta^+)$においてローカル整合性が成り立っていると呼ぶ。もし、複数の行動が\eqref{eq:tpcons}を満たすのであれば、どれを選んでもよい。つまり、状態価値を最大化するような行動を選ぶことは強制されない。しかし、$v^*$が実現可能で $\theta^+=\theta^*$ならば、 \eqref{eq:tpcons}を満たす任意の行動と、それに基づく方策が最適となる。

価値関数に基づく方策の緩和された記法を使うアドバンテージは、これを使うと、TensorPlanが価値関数が実現可能であるような任意の決定的方策と競えるようになることだ。これは、TensorPlanの範囲を拡張する。ひょっとするとTensorPlanに渡された特徴量ではと最適価値関数は実現可能ではないかもしれないが、もしある価値関数が実現可能であるような決定的方策が存在するならば、TensorPlanはその方策と同じだけの報酬を獲得できることが保証される。実際、TensorPlanは最適価値を達成する方策とほとんど同じくらい報酬を獲得できる。

TensorPlan

要約すると、仮説$\theta^+$を生成した後、TensorPlanは最初、シミュレータを使って何回かロールアウトをして、各状態$s$について\eqref{eq:tpcons}を満たす行動$a$を見つけられる。これが成功したら、TensorPlanはロールアウトを続け、$(s,a,h)$からの次状態をシミュレータから受け取り、$h$を一つ増やす。$h=H$になったら、ロールアウトを終了する。 TensorPlanはこのロールアウトを$m$回行い、もし全て成功したら、TensorPlanは停止してパラメタベクトル$\theta^+$ と、ロールアウトで使ったのと同じ方策$\pi_{\theta^+}$を使う。もしロールアウトの途中で非整合性が見つかった場合、TensorPlanは仮説集合$\Theta$を減らし次の実験を続ける。

(1) なぜTensorPlanが有限のクエリ回数で停止するのかと (2) なぜそれが健全なのかをこれから見ていこう。

TensorPlanは有限のクエリで停止するか？

さっそく, TensorPlanが有限のクエリで終了することを見ていこう. ここではパラメータの変化に伴う方策の変化が重要になってくる. まず, 次の記号$\Delta$を導入し, 以降ではしばしば$\Delta$を「判別子」と呼ぶ.

\[\begin{align*} \Delta(s,a,h,\theta) = r_a(s) + \langle P_a(s)\phi_{h+1},\theta \rangle - \phi_h(s)^\top \theta\,. \end{align*}\]

上の式の$\Delta(s,a,h,\theta)$は式 \eqref{eq:tpcons}の右辺と左辺の差に$v_h$と$v_{h+1}$の定義を代入し, さらに $P_a(s)\phi_{h+1} = \sum_{s'\in \mathcal{S}} P_a(s,s') \phi_{h+1}(s')\,;$ なる記号を用いて変形すると得られる. $P_a(s)\phi_{h+1}$ はつまり$(s,a)$が与えられたときの”次に期待される特徴ベクトル”である.

定義より, $\Delta(s,a,h,\theta)=0$を満たすような行動$a\in \mathcal{A}$が存在する場合のみ$(s,h,\theta)$で局所的な一貫性が成立する.

積の要素に一つでも０があれば結果が０になることを利用すれば、局所的な一貫性は $\begin{align} \prod_{a\in \mathcal{A}} \Delta(s,a,h,\theta) = 0\,. \label{eq:diprod} \end{align}$ と同一である.

このように局所一貫性を代数的に変形する理由は, $\Delta$の積が$(1,\theta^\top)^\top$の $A$-fold テンソル積の線形関数 として見ることができるためである.

これが成立するのを示すために, 新しい記法を導入しよう: 実数$r$と有限次元ベクトル$u$について, $(r,u^\top)^\top$というベクトルを$\overline{ r u}$として表記する (つまり, $r$を先頭に加え, $u$の要素を全て下にシフトしたもの). この記法を使うと, 判別子を内積として表すことができる.

\[\begin{align*} \Delta(s,a,h,\theta) = \langle \overline{r_a(s)\, (P_a(s)\phi_{h+1}-\phi_h(s))}, \overline{1 \, \theta} \rangle \end{align*}\]

次に, テンソル積 $\otimes$ についての表記を導入する (これは本文にはなくて論文にあったんですが, 本文だけだと全然わからなかったので追記しました) テンソル積 $\otimes: \mathbb{R}^{d_1} \times \mathbb{R}^{d_2} \rightarrow \mathbb{R}^{d_1 \times d_2}$ を $(u \otimes v)_{i \in\left[d_{1}\right], j \in\left[d_{2}\right]}=u_{i} \cdot v_{j}$として定義する. また, ベクトルの集合$\left(u^{(1)}, \ldots u^{(n)}\right)$, $n \in \mathbb{N}_{+}$について,

\[\left(\otimes_{i \in[n]} u^{(i)}\right)_{j_{1}, j_{2}, \ldots, j_{n}}=\prod_{i \in[n]}\left(u^{(i)}\right)_{j_{i}} \quad u^{(i)} \in \mathbb{R}^{d_{i}}\]

と表記する. さらに, この後ではしばしばテンソルを$vectorize$ 作用素を用いて, ベクトルとして扱っていく. つまり, テンソル$\mathbb{R}^{\times_{i \in[n]} d_{i}}$は$vectorize$によってベクトル$\mathbb{R}^{\prod_{i \in[n]} d_{i}}$として扱える. これを使って, $\left\langle\otimes_{i \in[n]} u^{(i)}, \otimes_{i \in[n]} v^{(i)}\right\rangle=\left\langle\text { vectorize }\left(\otimes_{i \in[n]} u^{(i)}\right), \operatorname{vectorize}\left(\otimes_{i \in[n]} v^{(i)}\right)\right\rangle$ と表記する. この表記を使うと, ベクトルについてのテンソル積 $\otimes$ が次の性質を満たす:

\[\begin{align*} \prod_a \langle x_a, y_a \rangle = \langle \otimes_a x_a, \otimes_a y_a \rangle\,, \end{align*}\]

この等式から, 式\eqref{eq:diprod} (つまり局所一貫性)は $\begin{align*} \langle \underbrace{\otimes_a \overline{r_a(s)\, (P_a(s)\phi_{h+1}-\phi_h(s))}}_{D(s,h)}, \underbrace{\otimes_a \overline{1 \, \theta}}_{F(\theta)} \rangle = 0\,. \end{align*}$ と一致する.

ここで, $F(\theta)\in \mathbb{R}^{(d+1)^A}$は$\theta$についての非線形関数だが, 上式は$F(\theta)$について線形であることに注意したい.

上式についてデータ$D(s,h)$が誤差０で獲得でき, $v^*$が実現可能である状況を考えよう. $k = (d+1)^A$とすると, $D(s,h)$ と $F(\theta)$ は $\mathbb{R}^k$ で値を取ることが分かる (これはシンプルにテンソルを展開している).

TensorPlanはシーケンス$(\theta_1,x_1), (\theta_2,x_2), \dots$を生成するアルゴリズムとみなすことができる. ここで, $\theta_i\in \mathbb{R}^d$ は$i$番目のTensorPlanによる仮説であり, $x_i\in \mathbb{R}^k$ が$i$番目の$(s, h)$についてのデータ$D(s,h)$である(このデータについてTensorPlanは非一貫性を検知している). 非一貫性が検知されると, 予想の集合は次のように縮小される:

\[\Theta_{i+1} = \Theta_i \cap \{ \theta\,:\, F(\theta)^\top x_i=0 \},\]

ここで, $\theta_{i+1}$ は $\Theta_{i+1}$ から式\eqref{eq:optplanning}によって選択される. $\Theta_1 = B_2^d(B)$ ($\mathbb{R}^d$についての半径$B$の$\ell^2$ボール)と合わせると, $i>1$について,

\[\Theta_i = \{ \theta\in B_2^d(B)\,:\, F(\theta)^\top x_1 = 0, \dots, F(\theta)^\top x_{i-1}=0 \}\]

が成立する.

$f_i = F(\theta_i)$としよう. $f_i$の成り立ちから, 任意の$i\ge 1$について, $\theta_i\in \Theta_i$ であり, $f_i$ は$x_1,\dots,x_{i-1}$に直行する. さらに, またしても$f_i$の成り立ちから, $x_i$ は not $f_i$には直行しない. これより, $x_i$ は$x_1,\dots,x_{i-1}$ が張る空間には含まれない　(含まれてしまうと, $f_i$に直行してしまうからだ). よって, $x_1,x_2,\dots$ は互いに独立である. $\mathbb{R}^k$には最大でも$k$個の線形に独立なベクトルが存在するので, Tensorplan は最大でも$k$個のデータのベクトルを生成する (実際にはTensorPlanは$k-1$個だけ生成する. なんでか分かるかな？). これはつまり, 最大でも$k$個の局所的一貫性についての”矛盾”の後, TensorPlanはこれ以上の非一貫性を検知するのをやめるため, 停止する.

Soundness

続いて, TensorPlanがSoundであることを見ていこう. $\theta^+$ をTensorPlanが停止するときに生成するパラメータベクトルとする. つまり, $m$回のロールアウトの中で, TensorPlanは一度も非一貫性を検知していない (なんで？).

$m$回のロールアウトの内, $i$回目のロールアウトで生成される軌跡$S_0^{(i)},A_0^{(i)},\dots,S_{H-1}^{(i)},A_{H-1}^{(i)},S_H^{(i)}$を考えよう. ここで非一貫性はないので, 任意の$0\le t \le H-1$について,

\[\begin{align} r_{A_t^{(i)}}(S_t^{(i)}) = v_t(S_t^{(i)};\theta^+)-\langle P_{A_t^{(i)}}(S_t^{(i)}), v_{t+1}(\cdot;\theta^+) \rangle\,. \label{eq:constr} \end{align}\]

が成立する.

よって, 確率 $1-\zeta$で,

\[\begin{align*} v_0^{\pi_{\theta^+}}(s_0) & \ge \frac1m \sum_{i=1}^m\sum_{t=0}^{t-1} r_{A_t^{(i)}}(S_t^{(i)}) - H \sqrt{ \frac{\log(1/\zeta)}{2m}} \\ & = \frac1m \sum_{i=1}^m\sum_{t=0}^{t-1} v_t(S_t^{(i)};\theta^+)-\langle P_{A_t^{(i)}}(S_t^{(i)}), v_{t+1}(\cdot;\theta^+)\rangle - H \sqrt{ \frac{\log(2/\zeta)}{2m}} \\ & \ge \frac1m \sum_{i=1}^m\sum_{t=0}^{t-1} v_t(S_t^{(i)};\theta^+)- v_{t+1}(S_{t+1}^{(i)};\theta^+) - (H+2B) \sqrt{ \frac{\log(2/\zeta)}{2m}} \\ & = v_0(s_0;\theta^+) - (H+2B) \sqrt{ \frac{\log(2/\zeta)}{2m}}\,, \end{align*}\]

が成り立つ. ここで, 最初の不等式はHoeffdingの不等式によるもので, 報酬が$[0,1]$であることを利用している. その後にある等式は式\eqref{eq:constr} を使っている. 2番目の不等式は, やはりHoeffdingの不等式によるものであり,$v_t$ が $[-B,B]$ であることと次の式を用いている.

\[\begin{align*} \langle P_{A_t^{(i)}} (S_t^{(i)}), v_{t+1}(\cdot;\theta^+)\rangle = \mathbb{E} [ v_{t+1}(S_{t+1}^{(i)};\theta^+) | S_t^{(i)},A_t^{(i)}] \end{align*}\]

(ここで, $v_t$ は $[0,H]$ に範囲を切り捨てて$H+2B$ を $2H$に置換できることに注意しよう). そして, 最後の等式は定義より$v_H(\cdot;\theta^+)=\boldsymbol{0}$ を使い, また, 定義より$S_0^{(i)}=s_0$を使っている. $m$ を十分大きくすると($m=\tilde O((H+B)^2/\delta^2)$),

\[v_0^{\pi_{\theta^+}}(s_0) \ge v_0(s_0;\theta^+)-\delta.\]

が保証できる.

これがSoundnessを意味することを見ていこう.

$\Theta^\circ \subset B_2^d(B)$ を, 決定的な方策$\pi$に対して$v^\pi = \Phi \theta$が成立するような$B$-bounded なパラメータベクトル $\theta$ の集合とする. $D$ と$F$の定義より, 任意の$i\ge 1$について, $\Theta^\circ \subset \Theta_{i}$ が成立する(正しい仮説は一度も除外されていない). これより, アルゴリズムのどの部分でも

\[v_0(s_0;\theta^+)\ge \max_{\theta\in \Theta^\circ} v^{\pi_{\theta}}_0(s_0)\]

が成り立つ.

よって, TensorPlanがパラメータ$\theta^+$で停止した時, 高い確率で,

\[v^{\pi_{\theta^+}}_0(s_0)\ge v_0(s_0;\theta^+)-\delta \ge \max_{\theta\in \Theta^\circ} v^{\pi_{\theta}}_0(s_0)-\delta\,.\]

が成立する.

特に, $v^*$ が $B$-実現可能である時, $v^{\pi_{\theta^+}}_0(s_0) \ge v^*_0(s_0)-\delta$ である. よって, 停止した後, 残りのエピソードについて, TensorPlan は$\theta^+$によって誘導される方策を安全に使うことができる.

Summary

今回はTensorPlanが$\Delta(s,a,h,\theta)$を誤差0で獲得できるかを見てきた. (1) 最大 $k$ 回の仮説集合の更新で停止する。 (2) 停止したとき，高い確率で，高い価値の方策を誘導するパラメータベクトルで戻ってくる．クエリ数については, $Delta(s,a,h, \theta)$を得ることを1クエリとした場合, TensorPlanは最大で $maH k =maH (d+1)^A$ クエリを必要とする ($m$ロールアウトについて, ロールアウトの$H$状態ごとに, $A$クエリーが必要である).

It remains to be seen how to adjust this argument to the case when $\Delta(s,a,h,\theta)$ need to be estimated based on interactions with a stochastic simulator. 確率的なシミュレータとの相互作用に基づいて$Delta(s,a,h, \theta)$ を推定する必要がある場合に, この議論をどう拡張するかは今後の課題である。

Notes

TensorPlanが計算機的に効率良く実装できるかは分かっていない. 私は多分できないと思っている. $\Theta_i$ がいくつかの複雑な非線形制約によって作られているためだ (パラメータベクトルについて).
今回の導出の本質は, 問題をより高次元の線形空間に持ち上げることである. これは機械学習の標準的な手法であるが, 線形予測器の能力を強化するためにデータを高次元空間に写像する場合は非常に異なる文脈となる. かつて流行ったRKHS法は、これを極端にしたものである。なお, 今回の導出は, 古典的なリフティングの手順とは対照的に, パラメータベクトルは非線形関数を通して高次元空間に写像される. 大事なのは, 学習が停止する理由を明確に把握することである.
ここで$Delta$を判別子と呼んだのは, この関数が「良い」ケースと「悪い」ケースを判別する目的で作られ, それを０という特別な値を使って行うためである. しかし, RLの文献に詳しい読者は, $$Delta$は, （ある固定された行動の下での）「TD誤差」として知られているものに過ぎないことに注意されたい.
このアルゴリズムは, パラメータベクトルの集合を制限するために使用する重要なデータについてデータバンクを構築し, そこに新しいデータを追加する際にかなり選択的になる面白い特徴がある. つまり, TensorPlanはリスト$x_1,x_2, \dots$に載るよりも多くのデータを生成する可能性がある. アルゴリズムを人に例えてしまえば, TensorPlanは「驚いたこと」を記憶していると言うことができるだろう. これはLSVI-$G$のような, 多くの冗長なデータを生成する可能性がある他のアルゴリズムとは非常に異なっている. もう一つの違いは, TensorPlanはデータから仮説集合を生成することである. この集合からのパラメータベクトルの選択は, TensorPlanが解く最適化（報酬最大化）問題によって決定される.
プランニングにおける楽観的アルゴリズムの例はかなり多い. また, 木探索に楽観性を使用した文献も多数ある. $A^*$アルゴリズムのような古典的なものも, 楽観的アルゴリズムと見なすことができる（少なくとも「許容ヒューリスティック」と併用する場合, これは$A^*$が値の楽観的推定値を使用しているというだけのことである）. LAO^*$$ アルゴリズムもその一つである。楽観的アルゴリズムのオンライン学習での本当の「故郷」はこのコースの後半で取り上げる予定だ.

Bibliographical notes

この講義は次の論文に基づいている:

Weisz, Gellert, Philip Amortila, Barnabás Janzer, Yasin Abbasi-Yadkori, Nan Jiang, and Csaba Szepesvári. 2021. “On Query-Efficient Planning in MDPs under Linear Realizability of the Optimal State-Value Function.”

arXivから読むことができる.