2. 基本定理

MDPの定義を総括し、前の講義で曖昧に終わらせた点をきちんと整理しよう。 なぜ確率分布\(\mathbb{P}_\mu^\pi\) が存在し、どのように定義すれば良いのだろうか？ 更に私たちが「動的計画法の基本定理」と呼ぶものを紹介し、価値反復法について議論しよう。

序論

マルコフ決定過程（Markov Decision Process, MDP） を5成分タプル $M = (\mathcal{S}, \mathcal{A}, P, r, \gamma)$とする。 ここで、$\mathcal{S}$は状態空間、$\mathcal{A}$は行動空間を表す。 $P = (P_a(s))_{s,a}$は （遷移のダイナミクスを表す）各状態と行動のペアに対する遷移先の状態分布の集合、 \(r= (r_a(s))_{s,a}\)はある状態においてある行動を実行した場合の即時報酬、 $0 \leq \gamma < 1$ は割引率を表す。前述したように、状態集合$\mathcal{S}$と行動集合$\mathcal{A}$は簡単のため有限とする。

方策 $\pi = (\pi_t)_{t \geq 0}$は無限列であり、各$t\ge 0$について、$\pi_t: (\mathcal{S} \times \mathcal{A})^{t-1} \times \mathcal{S} \rightarrow \mathcal{M}_1(\mathcal{A})$は長さ$t$の履歴に確率分布を割り当てる。 MDPにおいてある方策に従うということは、各時刻$t\ge 0$での行動の分布が、その時点での履歴に関わらず、方策で規定されるそれに従うということだ。

方策がMDPで使用される場合、方策とMDPのインターコネクションは、開始状態分布とともに、分布$\mathbb{P}$を形成する。これは状態行動対の無限列$S_0,A_0,S_1,A_1,\dots$、$S_0 \sim \mu(\cdot), A_t \sim \pi_t(\cdot | H_t)$に対し$S_{t+1} \sim P_{A_t}(S_t)$となるような分布だ。ただし$H_t = (S_0,A_0,\dots,S_{t-1},A_{t-1},S_t)$はある時刻$t$での履歴を表す。この方策とMDPのクローズドループでの相互作用（またはインターコネクション）を次図に示す。

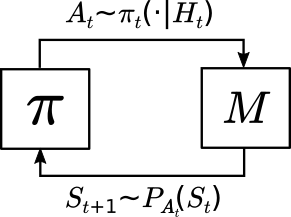
軌跡上の確率

前の講義で曖昧にした点の1つは、確率測度\(\mathbb{P}_\mu^\pi\)の存在だった。これについて、次の結果がある。

定理 (存在定理): 状態空間$\mathcal{S}$と行動空間$\mathcal{A}$で有限MDP $M$ を固定する。このとき、ある条件を満たす可測空間 $(\Omega,\mathcal{F})$と、$t\ge 0$での$S_t\in \mathcal{S}$, $A_t\in \mathcal{A}$から成る空間における確率変数列 $S_0, A_0, S_1, A_1, \ldots$ が存在する。 その条件とは、MDP $M$における任意の方策$\pi = (\pi_t)_{t \geq 0}$および$\mathcal{S}$上の任意の確率測度$\mu \in \mathcal{M}_1(\mathcal{S})$に対し、以下の条件を満たす$(\Omega,\mathcal{F})$上の確率測度$\mathbb{P}$が存在することだ。

1. 任意の $s \in \mathcal{S}$ に関して、$\mathbb{P}(S_0 = s) = \mu(s)$
2. 任意の $a \in \mathcal{A}, t \geq 0$ に関して、$\mathbb{P}(A_t = a | H_t) = \pi_t(a | H_t)$
3. 任意の $s’ \in \mathcal{S}$ に関して、$\mathbb{P}(S_{t+1} = s’ | H_t, A_t) = P_{A_t}(S_t, s’)$

証明: Ionescu-Tulcea theorem (“bandit book”の定理3.3)を使う。 \(\qquad\blacksquare\)

最後の条件3はマルコフ性とも呼ばれ、MDPの名前の由来となっている。多くの場合、$\Omega$を無限長の軌道の集合$\Omega = (\mathcal{S}\times \mathcal{A})^{\mathbb{N}}$として定義し、任意の$t\ge 0$に対して$S_t((s_0,a_0,s_1,a_1,\dots)) = s_t$、$A_t((s_0,a_0,s_1,a_1,\dots)) = a_t$として良い。結果として得られる確率空間は、MDP上の正規確率空間（より正確には、ある状態空間と行動空間上の正規確率空間）と呼ばれるものになる。ランダム性に関して他のソースが必要でない限り、$\Omega$をこの集合として定義できる。これは、$\mathbb{P}$の条件がすべて状態と行動の確率に関係しているためだ。正式には、写像$\omega \mapsto (S_0(\omega),A_0(\omega),S_1(\omega),A_1(\omega),\dots)$の下で$\mathbb{P}$の像測度をとる必要がある。

この定義は、$\mathcal{S}$と$\mathcal{A}$が$\sigma$-加法性を満たすことを暗示している。これは、${S_t = s}$と${A_t = a}$の両方が任意の$s\in \mathcal{S}$と$a\in \mathcal{A}$に対する(確率空間における)事象となるようにするためだ。

最適性といくつかの表記

慣例通り、確率測度$\mathbb{P}$の基礎となる期待値演算子を$\mathbb{E}$で表す。$\mu$や$\pi$への依存が重要な場合、$\mathbb{E}_\mu^\pi$と書く。文脈から明らかな場合、$\mu$や$\pi$を略記する。開始状態分布が単一の状態に集中している場合に、特別な注意を払おう。この状態を$s$とすると、開始状態分布は$\delta_s$と書ける。これはよく知られたディラックのデルタ分布で、状態$s$に原子がある場合だ。特別な注意を払う理由は、これがすべての開始状態分布（と実際には開始状態分布に線形に依存する量）の基礎を形成するためだ。 \(\mathbb{P}_{\delta_s}^{\pi}\)の略記に\(\mathbb{P}_{s}^{\pi}\)を使う。同様に、\(\mathbb{E}_{\delta_s}^{\pi}\)を\(\mathbb{E}_{s}^{\pi}\)と書く。

軌道上のリターン $\tau = (S_0, A_0, S_1, A_1, \ldots)$を以下のように定義する。

\[R = \sum_{t=0}^{\infty} \gamma^t r_{A_t}(S_t).\]

方策の価値関数$v^\pi$は状態を値に写像する。特に状態$s\in\mathcal{S}$について、$v^\pi(s)$ は$v^\pi(s) = \mathbb{E}_{s}^{\pi}[R]$によって定義される。これは、方策$\pi$とMDPとインターコネクションから成る分布と、開始状態$s$についての、リターンの期待値である¹。 $v^\pi(s)$がwell-definedとなることに注意しよう。これは、$v^\pi(s)$が、軌道$\tau$の関数である量の期待値だからだ。説明については、章末の注を参照してほしい。

MDPの標準的な目標は、すべての状態でこの値を最大化する方策を特定することだ。これを達成する方策は 最適方策として知られている。現時点では、最適方策が存在するかどうかは明らかではない。いずれにせよ、それが存在する場合、最適な方策は\(v^\pi = v^*\)を満たす必要がある。ここで、$v^*:\mathcal{S} \to \mathbb{R}$は次のように定義される。

\[v^{*}(s) = \sup_{\pi} v^{\pi}(s)\,, \qquad s\in \mathcal{S}\,.\]

最適価値関数の定義により、すべての$s \in \mathcal{S}$と任意の方策$\pi$に対して\(v^\pi(s) \leq v^{*}(s)\)が得られる。また、これを表すために$v^\pi \le v^*$を用いる。一般に、同じ定義域を持ち (例えば)実数の値をとる二つの関数 $f,g$ について $f \le g$ であるとは、 $f(z)\le g(z)$ が定義域における全ての可能な $z$ について成り立つことを言う。$f\ge g$ も同様に定義する。

また、ベクトルによって関数を表記し、そのベクトル空間上での演算を行えるものとする。特に明記されていない限り、すべてのベクトルは列ベクトルとする。記号$\boldsymbol{1}$を全ての要素が1のベクトルとして定義する。このベクトル $\boldsymbol{1}$ の長さは文脈に応じて変わる可能性がある。この講義では、これは$\mathrm{S}$次元のベクトルだとする。この記号は、多くの計算で非常に有用だ。これを使った定義から見ていこう。

近似的に最適な方策

$\varepsilon>0$とする。以下の条件が成り立つとき、方策$\pi$が$\varepsilon$ -最適であると言う。

\[v^\pi \ge v^* - \varepsilon \boldsymbol{1}\,.\]

$\varepsilon > 0$のとき、$\varepsilon$ -最適方策を見つけることは、最適方策を見つけるよりも直感的に簡単そうだ。

メモリーレス方策

最適な方策が過去の遷移を全て覚えておく必要がある場合、それらを計算できる効率的なアルゴリズムを発見することは絶望的だろう。それらを記述することでさえ無限の時間がかかってしまうかもしれない。幸いなことに、今はそうではない。有限MDPでは、最新の状態だけを使う方策を考えれば十分で、最適性を失わないとわかるだろう。これが後述するMDPの基本定理の主題だ。最新の状態のみを考慮した方策をメモリーレスな方策と呼ぶ。

正式には、メモリーレス方策は、状態から行動空間上の確率分布への写像として定義される：\(m: \mathcal{S}\to \mathcal{M}_1(\mathcal{A})\)。 $m$を使うと、以前の表記でのメモリーレス方策は$\pi_t(a|s_0,a_0,\dots,s_{t-1},a_{t-1},s_t) = m(a|s_t)$と書ける。ここで、$m(s_t)(a)$の代わりに$m(a|s_t)$を用いた。 したがって、名前から予想される通り、この方策は過去を「忘れ」、最新の状態に依拠して個々の行動に確率を割り当てる。メモリーレス方策とMDPとのインターコネクションによる分布の下で、状態と行動のペアの系列は、マルコフ連鎖を形成する。

以下、さらに表記を乱用し、メモリーレス方策に関しては、$\pi$が$m$を表すものとし、$\pi: \mathcal{S} \to \mathcal{M}_1(\mathcal{A})$と書く。

基本定理の証明を構築するため、(割引)訪問頻度の概念から見ていこう。

(割引)訪問頻度

開始状態の分布\(\mu \in \mathcal{M}_1(\mathcal{S})\)と方策\(\pi\)が与えられたとき、\(\mu\)と\(\pi\)および元となるMDP \(M\)による（割引）訪問頻度\(\nu_\mu^\pi \in \mathcal{M}_1(\mathcal{S} \times \mathcal{A})\)は次のように定義される。

\[\nu_\mu^\pi(s, a) = \sum_{t=0}^\infty \gamma^t \mathbb{P}_\mu^\pi (S_t = s, A_t = a).\]

興味深いことに、価値関数は、即時報酬関数$r$と訪問頻度$\nu_\mu^\pi$の間の内積として表すことができる。

\[\begin{align*} v^\pi(\mu) &= \mathbb{E}_\mu^\pi \left[ \sum_{t=0}^\infty \gamma^t r_{A_t}(S_t) \right] \\ &= \sum_{s, a} \sum_{t=0}^\infty \gamma^t \mathbb{E}_\mu^\pi \left[ r_{A_t}(S_t) \mathbb{I}(S_t = s, A_t = a) \right] \\ &= \sum_{s, a} r_{a}(s) \sum_{t=0}^\infty \gamma^t \mathbb{E}_\mu^\pi \left[ \mathbb{I}(S_t = s, A_t = a) \right] \\ &= \sum_{s, a} r_{a}(s) \sum_{t=0}^\infty \gamma^t \mathbb{P}_\mu^\pi(S_t = s, A_t = a) \\ &= \sum_{s, a} r_a(s) \nu_\mu^\pi(s, a) \\ &=: \langle \nu_\mu^\pi, r \rangle, \end{align*}\]

ここで、$\mathbb{I}(S_t = s, A_t = a)$は、事象${S_t=s,A_t=a}$に対する指示関数であり、事象が成り立つ場合（つまり、$S_t = s$および$A_t = a$）に1を、事象が成り立たない場合に0をとる。また、期待値の線形性から、最初の等式で$(s,a)$の総和を期待値の外に移動している。無限の合計を外側に移動する場合はより緻密に計算する必要がある。その場合、ルベーグの優収束定理に従えばよく、例えばLattimore & Szepesvári (2020) の第2章を参照してほしい。

上記の式から、特定の初期分布に対して報酬の期待値を最大化する問題は、報酬ベクトルrと最も良く一致するように占有率を「攪拌」する方策を選択する問題と同じだということがわかる。より報酬と一致するほど、方策の価値はより高くなる。これを下図に示す。

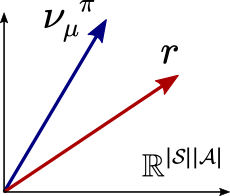
メモリーレス方策が最適制御に十分だと証明するために、次の結果が重要なステップとなる。

定理: 任意の方策$\pi$と開始状態分布$\mu \in \mathcal{M}_1(\mathcal{S})$に対して、次のようなメモリーレス方策$\pi’$が存在する。

\[\nu_\mu^{\pi'} = \nu_\mu^{\pi}.\]

証明（ヒント）： 最初に、状態空間\(\tilde{\nu}_\mu^\pi(s) := \sum_a \nu_\mu^\pi(s, a)\)上での訪問頻度を定義する。次に、以下のように定義された方策$\pi’$に対して定理の主張が成り立つことを示す。

\[\pi'(a | s) = \begin{cases} \frac{\nu_\mu^\pi(s, a)}{\tilde{\nu}_\mu^\pi(s)} & \text{if } \tilde{\nu}_\mu^\pi(s) \neq 0 \\ \pi_0(a) & \text{otherwise,} \end{cases}\]

ここで、\(\pi_0(a) \in \mathcal{M}_1(\mathcal{A})\)は任意の分布だ。 これを示すには、割引訪問頻度の定義から$\tilde \nu_\mu^\pi$を展開し、線形代数を用いる。

\[\tag*{$\blacksquare$}\]

得られるメモリーレス方策が、開始状態分布に依存することは重要だ。 メモリーレス方策により全ての状態について価値関数を再現できないような非メモリーレス方策が存在することについて、読者の方は納得してみてほしい。

ベルマン演算子と縮約

基本定理を述べる前に、最後にベルマン演算子として知られているものに関して、以下の定義と結果が必要だ。

メモリーレス方策$\pi$を修正しよう。 $\mathrm{S}$が$\mathcal{S}$の濃度（サイズ）であることを思い出してほしい。 まず、$r_\pi(s) = \sum_a \pi(a|s) r_a(s)$を、状態$s$が与えられた時の方策$\pi$のもとでの報酬の期待値として定義する。ここでも表記をオーバーロードし、$r_\pi \in \mathbb{R}^{\mathrm{S}}$が$s$番目の要素が\((r_\pi)_s = r_\pi(s)\)となるようなベクトルを表すものとする。 同様に、$P_\pi(s, s’) := \sum_a \pi(a|s) P_a(s, s’)$を定義し、$P_\pi \in [0, 1]^{\mathrm{S} \times \mathrm{S}}$が\(s\)行と\(s'\)列の要素について\((P_\pi)_{s, s'} = P_\pi(s, s')\)となるような確率的遷移行列を表すものとする。$P_\pi$の各行の合計が1になることに注意しよう。

\[P_\pi \mathbf{1} = \mathbf{1}\,.\]

$\pi$のもとでのベルマン/方策 評価演算子、$T_\pi: \mathbb{R}^{\mathrm{S}} \rightarrow \mathbb{R}^{\mathrm{S}}$は、以下のように定義される。

\[\begin{align*} T_\pi v(s) &= \sum_a \pi(a|s) \left \{r_a(s) + \gamma \sum_{s'} P_a(s, s') v(s') \right \} \\ &= \sum_a \pi(a|s) \left \{r_a(s) + \gamma \langle P_a(s), v \rangle \right \} \end{align*}\]

もしくは、短く以下のように表記する。

\[T_\pi v = r_\pi + \gamma P_\pi v,\]

ここで、$v \in \mathbb{R}^{\mathrm{S}}$だ。 ベルマン演算子は、価値関数に対して1ステップの先読み（ベルマン先読みとも呼ばれる）を実行する。表記$(T_\pi(v))(s)$, $T_\pi v(s)$、および\((T_\pi v)_s\)を同じ意味で用いる。$T_\pi$は、方策$\pi$の方策評価演算子としても知られている。

ベルマン最適性演算子 $T: \mathbb{R}^{\mathrm{S}} \rightarrow \mathbb{R}^{\mathrm{S}}$は以下のように定義される。

\[T v(s) = \max_a \{ r_a(s) + \gamma \langle P_a(s), v \rangle \}.\]

最大ノルムを\(\|\cdot\|_\infty\)により書く：\(\| v \|_{\infty} = \max_i |v_i|\)。 最大ノルムは、ベルマン演算子の「良き友人」だ。確率行列の演算子としての見方や「最大化」が、このノルムの「良い友達」であるためだ。結局、これらは以下の命題に帰着する。

命題（ベルマン演算子のγ縮約）： 任意の2つのベクトル$u, v \in \mathbb{R}^{\mathrm{S}}$と任意のメモリーレス方策\(\pi\)が与えられたとき、

1. \(\|T_\pi u - T_\pi v\|_\infty \leq \gamma \|u - v\|_\infty\) および
2. \(\|T u - T v\|_\infty \leq \gamma \|u - v\|_\infty\) が成り立つ。

この命題は初等的な代数によって証明でき、Szepesvári (2010)の付録A.2に完全な証明がある。

行動$a\in \mathcal{A}$について、演算子$T_a: \mathbb{R}^{\mathrm{S}} \to \mathbb{R}^{\mathrm{S}}$を、全ての状態で行動$a$を選択するメモリーレス方策$T_\pi$と一致するものとして定義すると便利だ。もちろん、ただの特殊なケースなので、上記の収縮特性も満たしている。これは、固定した行動で1ステップ先読みしていると見なすことができる。

バナッハの不動点定理から、次の結果が得られる。

命題（不動点反復）： 任意の$u \in \mathbb{R}^{\mathrm{S}}$と任意のメモリーレス方策$\pi$が与えられたとき、

1. \(v^\pi = \lim_{k\to\infty} T_\pi^k u\)の時、任意の$k\ge 0$について、\(\| v^\pi - T_\pi^k u \|_\infty \le \gamma^k \| u - v^\pi \|_\infty\)が成り立つ。ここで \(v^\pi\) は、 \(T_\pi v^\pi = v^\pi\)を満たすユニークなベクトル/関数である。
2. \(v_\infty=\lim_{k\to\infty} T^k u\)がwell-definedである時、任意の$k\ge 0$について, \(\| v_\infty - T^k u \|_\infty \le \gamma^k \| u - v_\infty \|_\infty\)が成り立つ。また、\(v_\infty\) は、\(Tv_\infty = v_\infty\)を満たすベクトル/関数であり、一意に定まる。

---

基本定理

定義 あるメモリーレス方策$\pi$が、全ての状態$s\in \mathcal{S}$において確率1で$(T_a v)(s)=r_a(s) + \gamma \langle P_a(s), v \rangle$を最大化させる行動をとる時、価値関数$v: \mathcal{S} \rightarrow \mathbb{R}$について貪欲であると言う。 (1ステップ)ベルマン先読み$(T_a v)(s)$を最大化する行動が、2つ以上あるかもしれないことに注意しよう (引き分けがある場合だ)。実際、引き分けはとてもありふれたものだ。全ての状態で「行動のダブり」がある場合を想像してみよう。つまり、ある行動と同じ遷移と報酬になるように、コピーの行動を作ってしまえばいい。もしコピー元の行動がベルマン先読みをある状態で最大化するなら、新しい行動もそうするだろう。 行動はたくさんあるかもしれないが有限なので、ベルマン先読みを最大化させるようなものは必ず存在する。それゆえ、いずれかの$v\in \mathbb{R}^{\mathrm{S}}$に従って、常に貪欲な方策を「とってくる」ことができるのだ。

命題 (貪欲性の特徴づけ) あるメモリーレス方策$\pi$が$v\in \mathbb{R}^{\mathrm{S}}$について貪欲であるのは、

\[T_\pi v = T v\,\]

が成り立つ場合のみである。

これで、MDPの基本定理と私が呼ぶものを主張する準備ができた。

定理 (MDPの基本定理): 任意の有限MDPについて、以下が成り立つ。

1. $v^*$について貪欲であるような任意の方策は最適であり、\(v^\pi = v^*\)が成り立つ;
2. \(v^* = T v^*\) が成り立つ。

等式 $v=Tv$ は ベルマン最適方程式 として知られているものだ。なので2. の結果は、最適価値関数はベルマン最適方程式を満たす、と言いかえてよい。 また、前の不動点についての命題でもすでに、ベルマン方程式が登場している。そこでの結果は\(v^*\)を近似的に計算する方法を暗に示しているが、これは証明の後で確認しよう。

証明:

$v^*$の定義でメモリーレス方策のみを考慮すれば、証明は難しくない。ここで、$\text{ML}$が与えられたMDPにおけるメモリーレス方策の集合を表すものとして、以下を定義しよう。

\[\tilde{v}^*(s) = \sup_{\pi \in \text{ML}} v^\pi(s) \quad \text{for all } s \in \mathcal{S}\,.\]

もうすぐ見ることになるが、この定理の$v^*$を\(\tilde{v}^*\)で置きかえた定理を示すのは難しくない。 つまり、

1. $\tilde{v}^*$について貪欲であるような任意の方策は最適であり、\(v^\pi = \tilde{v}^*\)が成り立つ;
2. \(\tilde{v}^* = T \tilde{v}^*\) が成り立つ。

これは私たちが証明のパート1で示すものだ。パート2では、\(\tilde{v}^*=v^*\)を示す。 この2つのパートを組み合わせれば望みの結果が得られることは明らかだろう。

パート 1: 証明のアイデアは、まず以下を示すことだ。 \(\begin{align} \tilde{v}^*\le T \tilde{v}^* \label{eq:suph} \end{align}\) それから$\tilde{v}^*$に関する任意の貪欲方策$\pi$ について \(v^\pi \ge \tilde{v}^*\) を示せばよい。

\(\eqref{eq:suph}\)を示すにはまず、全てのメモリーレス方策$\pi$について \(v^\pi \le \tilde{v}^*\) が成り立つことを言う。これは定義から従う。両辺にベルマン演算子$T_\pi$を適用すると、$v^\pi = T_\pi v^\pi$より、$v^\pi \le T_\pi \tilde{v}^*$を得る。この式の両辺を$\pi$について最大化すると、$T v = \sup_{\pi \in \text{ML}} T_\pi v$が任意の$v$について成り立つ。これと\(\tilde{v}^*\) の定義から、\(\eqref{eq:suph}\)が言える。

いま、\(\tilde{v}^*\)について貪欲な任意のメモリーレス方策$\pi$をとってこよう。すなわち、\(T_\pi \tilde{v}^* = T \tilde{v}^*\)だ。

\(\eqref{eq:suph}\)と合わせて、以下を得る。

\[\begin{align} \label{eq:start} T_\pi \tilde{v}^* \ge \tilde{v}^*\,. \end{align}\]

$T_\pi$を両辺に適用する。$T_\pi$が不等号をそのままに保つことに注意しよう (つまり、$u\le v$であるような任意の$u,v$について$T_\pi u \le T_\pi v$だ)。

\[T_\pi^2 \tilde{v}^* \ge T_\pi \tilde{v}^* \ge \tilde{v}^*\,,\]

ここで、最後の不等式は\(\eqref{eq:start}\)から従う。同様の理由で、任意の$k\ge 0$についてもこれを得る。

\[T_\pi^k \tilde{v}^* \ge T_\pi^{k-1} \tilde{v}^* \ge \dots \ge \tilde{v}^*\,,\]

いま、不動点定理の命題より、不動点反復 $T_\pi^k \tilde{v}^*$ は $v^\pi$ に収束する。よって、極限をとって、以下を得る。

\[v^\pi \ge \tilde{v}^*.\]

これと、\(v^\pi \le \tilde{v}^*\) より、\(v^\pi = \tilde{v}^*\) が言える。

よって、$T \tilde{v}^* = T_\pi \tilde{v}^* = T_\pi v^\pi = v^\pi = \tilde{v}^*$ が成り立つことがわかった。

パート2: さて、\(\tilde{v}^* = v^*\) の証明が残っている。 $\Pi$ を全ての方策の集合だとしよう。 $\text{ML}\subset \Pi$なので、 \(\tilde{v}^*\le v^*\)だ。 よって、以下を証明すれば良い。

\[\begin{align} \label{eq:mlbigger} v^* \le \tilde{v}^*\,. \end{align}\]

これを示すには、任意の開始状態分布$\mu$と方策$\pi$ (メモリーレスでないものも含む)について、メモリーレス方策を見つけられるという定理を使う。いま、$\pi$に対応するメモリーレス方策($\nu_\mu^\pi = \nu_\mu^{\text{ML}}$が成り立つようなもの)を$\text{ML}(\pi)$と書く。適当に状態$s\in \mathcal{S}$をとってこよう。この結果を$\mu = \delta_s$に適用して、以下の結果を得る。

\[\begin{align*} v^\pi(s) & = \langle \nu_s^\pi, r \rangle \\ & = \langle \nu_s^{\text{ML}(\pi)}, r \rangle \\ & \le \sup_{\pi'\in \text{ML}} \langle \nu_s^{\pi'}, r \rangle \\ & = \sup_{\pi'\in \text{ML}} v^{\pi'}(s) = \tilde{v}^*(s)\,. \end{align*}\]

両辺を $\pi$について最大化して、 \(v^*(s)= \sup_{\pi\in \Pi} v^\pi(s) \le \tilde{v}^*(s)\)を得る。$s\in \mathcal{S}$ は任意の状態なので、\(v^*\le \tilde{v}^*\) を得る。よって証明できた。 \(\qquad\blacksquare\)

証明の中で登場した性質で、この後も繰返し使うものに、$T_\pi$が単調な演算子であるという性質がある。これは$T$についても成り立つ。参考までに、これを命題として書いておく。

命題 (ベルマン演算子の単調性): 任意のメモリーレス方策$\pi$と、$u\le v$であるような任意の$u,v\in \mathbb{R}^{\mathrm{S}}$について、$T_\pi u \le T_\pi v$が成り立つ。同様にベルマン最適演算子$T$についても成り立つ。

MDPの基本定理から、最適価値関数\(v^*\)にアクセスできる場合、最適方策を効率的かつ効果的な方法で見つけられる。ただ価値関数を貪欲化 (greedification、価値関数について貪欲な方策を計算)すればいい: (方策の記法を乱用して) \(\pi(s) = \arg\max_{a \in \mathcal{A}} \{r_a(s) + \gamma \langle P_a(s), v^* \rangle \} \quad \forall s \in \mathcal{S}\)。そのような貪欲方策は$O(\mathrm{S}^2 \mathrm{A})$の計算時間で見つけられる。

よって、もし効率よく最適価値関数を見つけられるのなら、最適方策も効率よく計算できる。これは最適方策を見つけるためのナイーブな手法、つまり方策を全列挙し価値関数が最大のものを見つける手法とは対照的だ。

しかし、たとえ決定的な方策だけを考慮した場合でも、そのような方策は$\Theta(\mathrm{A}^{\mathrm{S}})$のオーダーで存在しているため、コストのかかる手続きになってしまう。

結論から言うと、有限のMDPでは、最適方策を$\mathrm{S}$、$\mathrm{A}$、$1/(1-\gamma)$の多項式オーダーで計算する手法が存在し、ナイーブな手法で見られるような、状態数にともなう指数的な計算時間の増加は避けることができる。 これを実現できるのは、動的計画法と呼ばれるアルゴリズムの一族に属するアルゴリズムだ。 私たちの用途では、計算する時に状態価値をトラッキングする (つまり、価値関数を使う)というアイデアを使う任意の手法を動的計画法と呼ぶ。

基本定理は驚くべきものだ。どうして私たちは価値関数の値が他の方策よりも大きいような方策を見つけられるのだろうか？基本定理は、どういうわけか、あるMDPでは全ての価値関数 ($V^\pi$)の部分集合 ($\mathbb{R}^{\mathrm{S}}$の中の集合)が、とても特別なものだと教えてくれる： 価値関数全体の超多面体を考えた時に、最適価値関数は、他の価値関数を従える頂点になるのだ[^note-vertex]。これはとても魅力的だ。もちろん、鍵となるのはマルコフ性であり、このおかげで、任意の方策からメモリーレスなものに移ってもよいという結果が得られる。

価値反復法

基本定理から、\(v^*\)は$T$の不動点になる。先ほどのバナッハの不動点定理についての命題から、列\(\{T^k v\}_{k\ge 0}\) は指数的に\(v^*\)に収束する。 MDPの文脈では、$T$を繰返しある関数に適用することは、価値反復法と呼ばれる。 最初の価値関数はふつう全て0で初期化され、これを$\mathbf{0}$と書く。しかし、もちろんより良い \(v^*\)についての推察があれば、その推察を初期値に使ってもいい。 次の結果は、$v^*$ の $\varepsilon$-近傍 (最大ノルムについて)に到達するまでのイテレーションの回数について、上限を与える。

定理 (価値反復法): 即時報酬が$[0,1]$の範囲でバウンドされているMDPを考えよう。 任意の正の数$\varepsilon>0$をとってくる。 $v_0 = \boldsymbol{0}$として、\(v_{k+1}\)を以下のように定義する。

\[v_{k+1} = T v_k \quad \text{for } k = 0, 1, 2, \ldots\]

すると、$k\ge \ln(1/(\varepsilon(1-\gamma))/\ln(1/\gamma)$について、\(\|v_k -v^*\|_\infty \le \varepsilon\)が成り立つ。

証明の前に、以下の結果を思い出そう。²

\[H_{\gamma,\varepsilon}:= \frac{\ln(1/(\varepsilon(1-\gamma)))}{1-\gamma} \ge \frac{\ln(1/(\varepsilon(1-\gamma)))}{\ln(1/\gamma)}\,.\]

ここで1章で登場したエフェクティブホライゾン $H_{\gamma,\varepsilon}$が再び登場した。もちろん、これは偶然ではない。

証明: 報酬に関する仮定から、$\mathbf{0} \le v^\pi \le \frac{1}{1-\gamma} \mathbf{1}$が任意の方策$\pi$に関して成り立つ。よって、\(\|v^*\|_\infty \le \frac{1}{1-\gamma}\)もまた成り立つ。 不動点反復の命題から、以下を得る。

\[\begin{align*} \|v_k - v^*\|_\infty &\leq \gamma^k \|v^* - \mathbf{0}\|_\infty = \gamma^k \|v^*\|_\infty \leq \frac{\gamma^k}{1 - \gamma} \,. \end{align*}\]

\(\gamma^k/(1-\gamma)\le \varepsilon\) を満たすような最小の$k$を解く³と、証明したい結果を得る。

\[\tag*{$\blacksquare$}\]

ある固定された$\gamma<1$について、反復複雑性が目標とする近似率$\varepsilon$に対し、緩くしか依存していないことに注意しよう。なので、$v^*$の近傍にいくまで、たった少しのイテレーションを回すだけでいい。また、時間計算量が$O(\mathrm{S}^2 \mathrm{A}k)$、空間計算量が$O(\mathrm{S})$になることにも注意しよう。ただし価値が$O(1)$のメモリしか消費しないこと、算術・論理演算が$O(1)$の時間しか要求しないことを仮定している。

要求される正確さは、余計に足される誤差の形で表れてくる。 最適価値関数\(v^*\)が$1/(1-\gamma)$ (報酬が常に最大値の1をとる場合だ)のオーダーなら、相対的な近似率のオーダーが$2$というのは、$\epsilon=0.5/(1-\gamma)$を意味し、時間計算量は$\ln(2)/(1-\gamma)$のオーダーになる。 しかし、相対誤差を制御するのにもっと興味深いケースは、\(v^*\)が小さい値をとるときだ。この時、反復複雑性の上限はバウンドできなくなってしまう。⁴ 後に、このようにきめ細かく誤差を制御できない性質のため、価値反復法は最適方策を厳密に求めるのには向かないということを確認しよう。

ノート

価値関数はwell-defined

本文にあったように、確率空間$(\Omega,\mathcal{F},\mathbb{P})$が一意に定まらないにも関わらず、価値関数はwell-definedだ。 実際、任意の (可測)関数 $f: (\mathcal{S}\times \mathcal{A})^{\mathbb{N}} \to \mathbb{R}$ と 任意の確率空間$(\Omega,\mathcal{F},\mathbb{P})$、$(\Omega’,\mathcal{F}’,\mathbb{P}’)$ について、 $\mathbb{P}$ と $\mathbb{P}’$ が 存在定理で仮定された要求を満たすなら、 \(\int f(\tau(\omega)) \mathbb{P}(d\omega)=\int f(\tau(\omega)) \mathbb{P}'(d\omega)\)、 または$\mathbb{P}$のもとでの期待値$\mathbb{E}$ (と$\mathbb{P}’$については$\mathbb{E}’$)を導入して、 \(\mathbb{E}[f(\tau)]=\mathbb{E}'[f(\tau)]\) が成り立つ。 また、軌道上での確率と期待値が必要であれば、$(\Omega,\mathcal{F},\mathbb{P})$を、MDPの状態-行動空間での正規確率空間でいっぺんにとってやれば大丈夫だ。

他の種類のMDP

他にどんなMDPが生き残ってきたのか？というのは、よくある疑問だろう。例えば、有限ホライゾンのMDPや、 時間定常な・時間定常でないMDP、割引がある・割引がないMDP、総コスト (つまり、報酬は全て負の値)が目標のMDP、または平均報酬の設定などはどうだろうか？ 解答としては、これらのMDP上でも理論を作れるのだが、自動的にそのまま、というわけにはいかない。よく研究されている主題なので、後で参照とヒントを示す予定だ。もしかしたら直接の構成もするかもしれない。

無限の空間ではどうなるか？

(状態数が)無限の空間で、まず始めに変更しないといけないことは、報酬の上限/下限がバウンドされているという仮定をそのまま使えないことだ。これはいくぶん面倒な問題を引きおこしてしまう: いくつかの方策については、$v^\pi$ がバウンドできないのだ。$v^*$ についても同じだ。負の無限大に発散する価値はとりわけ”有害”だ (LQR制御は、これが出てくる最も簡単な例だろう)。 もう一つ、貪欲方策の存在をそのまま使えないことも問題だ。これは行動数が無限の場合では既に問題になっている⁵。$a>0$に対し$r_a(s)=1-1/a$を最大化する行動とは何だろう？ということだ。 しばしば、報酬のコンパクト性と遷移関数の連続性の仮定を課すことでこれを解決できる。 こうして近似された貪欲性が十分なのかは全く自明ではないが、実際のところ、後で見るように、近似的に最適な計算だけ考慮するならこれで十分だ。

最後に、状態と行動がどちらも非加算無限であるような場合は、方策の定義に注意を払う必要がある。 いま、遷移確率に制約を課そう。 状態空間と行動空間の両方に、可測な構造を入れてやればよい (これは、状態集合と行動集合のどちらかが加算な濃度よりも大きい濃度を持っているときのみ重要になる)。 ここでの主な変更は、そのような写像があれば、$h_t \mapsto \pi_t(U|h_t)$は$U$($A$の可測な部分集合)の選択に関わらず可測であるということだ。これにより、Ionescu-Tulcea定理(存在定理で使ったもの)が使えるようになり、少なくとも定義はできるようになる。 また2つ目の困難は、「貪欲化」により計算した方策が、こうして定義した可測な方策の集合からはみ出してしまうことだ。これに対処するためにも、多くの研究がなされてきた。

無限長の軌道から有限のプレフィックスへ

軌道は無限長になってもよいので、方策とMDPとのインターコネクションについて、確率測度が存在するという非構成的な結果が得られたのだった (存在定理)。 私たちはしばしば、この無限長の軌道の上で、2つの確率測度が同一のものか確める必要がある。 どうやってやればよいだろうか？ 測度論の一般的な結果によれば、ある軌道のもととなる$\sigma$-加法族の生成族が同じなら、そのような2つの確率測度は同じになる。 軌道上の$\sigma$-加法族の(正規確率空間となるように)生成族として、便利な例は、ある$s_0,a_0,\dots,s_t,a_t,\dots$について、要素が以下の2つの集合の直積からなるものだ。

\[\begin{align*} & \{s_0\} \times \{a_0\} \times \dots\times \{ s_t \} \times \mathcal{A} \times (\mathcal{S}\times \mathcal{A})^{\mathbb{N}} \\ & \{s_0\} \times \{a_0\} \times \dots\times \{ s_t \} \times \{a_t\} \times (\mathcal{S}\times \mathcal{A})^{\mathbb{N}} \end{align*}\]

つまり、もし $\mathbb{P}$ と $\mathbb{P}’$ がこれらの集合について同じ値をとるなら、この2つはどこでも同じということだ。 これにより、結果が1つの円環を成してくる: この結果が意味するのは、無限長の軌道が持つ有限長のプレフィックスに対して割り当てられた確率だけをチェックすればいいということだ。ヒュー。 これらの有限長のプレフィックスに対して割り当てられた確率は、$\mu, P, \pi$の関数になるので、 軌道の空間上の一意な確率測度 $ (\mathcal{S}\times \mathcal{A})^{\mathbb{N}}$ で、存在定理で仮定された要求を満たすものが存在するという結果が従う。 つまり、正規確率空間は一意に定義される。

基本定理

BertsekasとSheveの本では、私が基本定理と呼んだ定理を著者らが同じ名前で呼んでいたと思う。 しかし、これはあまり標準的な名前ではない。それでも、この結果は重要で、他の結果がたくさんこの結果から従ってくる。ある意味、これは全ての理論の核となる結果なのだ。なので私は、この名前がふさわしいと思う。 たぶん私はこの証明をどこかで読んだと思うのだが、ずいぶん前のことで、どこだか忘れてしまった。強化学習分野の人々は、よくメモリーレス方策から始めて\(v^*\)よりも\(\tilde{v}^*\)を考える。 \(\tilde{v}^*=v^*\)が成り立つのかという疑問は、制御理論やオペレーションリサーチの分野では、よく研究され理解されてきた。

バナッハの不動点定理

この定理は私の短い強化学習本 (Szepesvári, 2010)の付録 A.1で見つかるだろう。 しかし、もちろん、多くの場所に載っているものだ (Wikipediaの記事でもいい)。 コーシー列の概念 (これは振動が消えていく列と呼ばれるべきだろう)や実数の完備性に立ち返って、この定理が成り立つ条件を理解するのに少しの時間を費すのは、価値のある行為だ。

参考文献

参照した文献は以下の通りだ。

• Lattimore, T., & Szepesvári, C. (2020). Bandit algorithms. Cambridge University Press.
• Szepesvári, C. (2010). Algorithms for reinforcement learning. Synthesis lectures on artificial intelligence and machine learning, 4(1), 1-103.

次に示す本の章は、MDPについてわりあい網羅的だが簡潔な紹介をしている。この章はまたマルコフ方策の十分性を通して、基本定理の証明を、割引ケースといくつかの最適性基準のもとで行っている。

• Garcia, Frédérick, and Emmanuel Rachelson. 2013. “Markov Decision Processes.” In Markov Decision Processes in Artificial Intelligence, 1–38. Hoboken, NJ USA: John Wiley & Sons, Inc.

加算なボレル状態集合・ボレル行動集合を持ち、報酬関数の下限が[^todo-from-below]バウンドできないMDPについての基本的な結果が、以下の(素晴らしい)論文にある。またそれらの結果についての簡単な歴史も載っている。

• Feinberg, Eugene A. 2011. Total Expected Discounted Reward MDPS: Existence of Optimal Policies.. In Wiley Encyclopedia of Operations Research and Management Science. Hoboken, NJ, USA: John Wiley & Sons, Inc.

翻訳者注

---