14. Politex
前回の講義の最後に導いた計算結果から以下の定理が得られる:
補題 (混合方策の準最適性): MDP $M$を固定する. 任意の方策の系列\(\pi_0,\dots,\pi_{k-1}\), 関数の系列 $\hat q_0,\dots,\hat q_{k-1}: \mathcal{S}\times \mathcal{A} \to \mathbb{R}$, およびメモリーレス方策\(\pi^*\)に対して, 混合方策 $\bar \pi_k = (\pi_0+\dots+\pi_{k-1})/k$ は次の式を満たす:
\[\begin{align} v^{\pi^*} - v^{\bar \pi_k} & \le \frac1k (I-\gamma P_{\pi^*})^{-1} \underbrace{ \sum_{j=0}^{k-1} \left( M_{\pi^*} \hat q_j - M_{\pi_j} \hat q_j \right)}_{T_1} + \frac{2 \max_{0\le j \le k-1}\| q^{\pi_j}-\hat q_j\|_\infty }{1-\gamma} \,. \label{eq:polsubgapgen} \end{align}\]この補題における唯一の制約は方策$\pi^*$についてのみで, $\pi^*$がメモリーレス方策でないといけないということである. 混合方策の準最適性を抑えるには, 行動価値の近似誤差\(\| q^{\pi_j}-\hat q_j\|_\infty\)と$T_1$の項を(上から)抑えれば充分で, \(\pi_0,\dots,\pi_{k-1}\)は自由に選んでよい. どのような方策の系列を選べばよいか考えるため, 固定した状態$s$について、\(T_1(s)\)を調べよう:
\[\begin{align} T_1(s) = \sum_{j=0}^{k-1} \langle \pi^*(s,\cdot) - \pi_j(s,\cdot) ,\hat q_j(s,\cdot)\rangle \,, \label{eq:t1s} \end{align}\]ここでは略記のために, \(\pi(a|s)\)に\(\pi(s,a)\)を使う. \(\hat q_j\)が\(\pi_j\)に基づいて計算されるが, 一方で\(\pi^*\)は未知であることを思い出そう. この項を抑えることは可能なのだろうか?
オンライン線形最適化
偶然にも, このような項を上から抑えるという問題は, 学習理論の一分野のオンライン学習で研究されている中心的な問題だ. 特にオンライン線形最適化では以下の問題が研究されている:
敵対者と学習者が$k$ラウンドの交互手番二人零和ゲームを行う. ラウンド$j$ ($0\le j \le k-1$)において, まず学習者がベクトル\(x_j\in \mathcal{X}\subset \mathbb{R}^d\)を選ぶ. そして敵対者はベクトル\(y_j \in \mathcal{Y}\subset \mathbb{R}^d\)を選ぶ. この選択の前に敵対者は学習者の過去の全ての選択について知っており, 学習者も敵対者の過去の全ての選択について知っている. また両者は自身の選択も記憶している. 簡単のため, 両者の選択は決定的だとしよう. $k$ラウンド後のこの敵対者に与えられる利得は以下の式で表される
\[\begin{align} R_k = \max_{x\in \mathcal{X}}\sum_{j=0}^{k-1} \langle x - x_j, y_j \rangle\,. \label{eq:regretdefolo} \end{align}\]ゲームが零和なので, 敵対者のゴールはこれを最大化することで, 学習者のゴールはこれを最小化することだ. 敵対者と学習者の両方は$k$と集合$\mathcal{X},\mathcal{Y}$を与えられる. $L$が学習者の戦略($\mathcal{X}$に対する履歴のマップの系列)を表現しており, $A$は敵対者の戦略($\mathcal{Y}$に対する履歴のマップの系列)を表すとしよう. 上記の利得は$L$と$A$に依存している: $R_k = R_k(A,L)$.
学習者の立場をとると, \eqref{eq:regretdefolo}で定義された数値は学習者のリグレットと呼ばれる. ゲームのミニマックス値 \(R_k^*\) は \(R_k^* = \inf_L \sup_A R_k(A,L)\) で与えられる.
したがって \(R_k^*\) は \(k\), \(\mathcal{X}\) そして \(\mathcal{Y}\) にのみ依存する. コンテキストから \(k\), \(\mathcal{X}\), \(\mathcal{Y}\) が明らかなら, 表記からそれらを省く. 重要な問題は $R_k^*$ が $k$, そして $\mathcal{X}$ と $\mathcal{Y}$ にどのように依存するのかということである. オンライン線形最適化では集合$\mathcal{X}$ と $\mathcal{Y}$の両方は凸とする.
我々が考えている問題においては, \(d=\mathrm{A}\), \(\mathcal{X} = \mathcal{M}_1(\mathrm{A}) = \{ p \in [0,1]^{\mathrm{A}} \,:\, \sum_a p_a = 1 \}\) を \(\mathbb{R}^{\mathrm{A}}\) における \(\mathrm{A}-1\) 次元確率単体, \(\mathcal{Y} = [0,1/(1-\gamma)]^{\mathrm{A}}\)とすると, \eqref{eq:t1s}の\(T_1(s)\) が \eqref{eq:regretdefolo} のリグレットの定義に一致する. \(\hat q_j(s,\cdot)\) は敵対的に選ばれるわけではないが, 任意の選択に対して成立するリグレットのバウンドは, 特定の選択におけるバウンドとしても使える.
鏡像降下法 (Mirror Descent)
鏡像降下法 (MD) は最適化理論に起源を持つアルゴリズムの一つである. オンライン線形最適化の文脈では MDは幅広い状況下で学習者のリグレットがミニマックスリグレットに近いことが保証される戦略だ.
多くのオンライン線形最適化に関する文献に合わせるため, $y_j$の正負を切り替えると都合がよい. したがって今後は, 学習者は \(\langle x,y \rangle\) を \(x\in \mathcal{X}\) の選択により最小化することを目指し, 敵対者は同じものを \(y\in \mathcal{Y}\) の選択により最大化することを目指すと仮定する. (前セクションでは, 学習者は \(\langle x,y \rangle\) の最大化, 敵対者はそれの最小化を目指していたことに注意.) これはリグレットも以下の形に再定義することを意味する.
\[\begin{align} R_k & = \max_{x\in \mathcal{X}}\sum_{j=0}^{k-1} \langle x_j - x, y_j \rangle \nonumber \\ & = \sum_{j=0}^{k-1} \langle x_j, y_j \rangle - \min_{x\in \mathcal{X}} \sum_{j=0}^{k-1}\langle x,y_j \rangle\,. \label{eq:regretdefololosses} \end{align}\]他は全て同じままだ. すなわちゲームは零和ミニマックスゲームで, リグレットは敵対者の利得であり, 負のリグレットは学習者の利得である. このケースは損失ゲームと呼ばれる. 損失ゲームが好まれる理由は多くの 最適化理論が凹関数の最大化よりも凸関数の最小化の形で記述されるからである. しかし, どちらを選ぶかは自由である. 二行目のリグレットの形式は, プレイヤーの目標が, 敵対者の全ての選択を考慮して得られた \(\mathcal{X}\) の最良単一決定と競うことであることを示している. つまり学習者の目標は, 総損失 \(\sum_{j=0}^{k-1} \langle x_j, y_j \rangle\) を 最良総損失 \(\min_{x\in \mathcal{X}} \sum_{j=0}^{k-1}\langle x,y_j \rangle\) に近いか, より小さく保つことだ. (この記法においては, \(\mathcal{Y} = [-1/(1-\gamma),0]^{\mathrm{A}}\) とすると $T_1(s)$ は \(R_k\) に一致する.)
MDは再帰的に定義されており, 最も簡単な形式では二つの設計パラメータを持つ. 一つ目は拡大実数凸関数 \(F: \mathbb{R}^d \to \bar {\mathbb{R}}\) であり, これは”正則関数”と呼ばれる. 一方で二つ目はステップサイズあるいは学習率パラメータ $\eta>0$ である. (拡大実数は \(\mathbb{R}\) に \(+\infty, -\infty\) を追加し, それらと実数の基本的な計算を適切に拡張したものだ. 凸関数が \(+\infty\) をとることを許容することで, 目的関数と”制約”を円滑に融合できる. 負の拡大実数凸関数にもしばしば取り組む必要があるため, 負の無限大 $-\infty$ も追加した.)
MDは次のようなアルゴリズムだ. まずラウンド$0$では, \(F\) を最小化する $x_0\in \mathcal{X}$ を選ぶ:
\[x_0 = \arg\min_{x\in \mathcal{X}} F(x)\,.\]以下では, MDの定義で必要となる最小点が常に存在することを前提とする. 我々が必要とする場合では, \(\mathcal{X}\) は \(d-1\) 次元確率単体であり, これは閉凸集合である. そして凸関数は連続であるため, 最小点は常に存在を保証される.
そしてラウンド \(j>0\) では, MDは以下の \(x_j\) を選ぶ:
\[\begin{equation} \begin{split} x_j & = \arg\min_{x\in \mathcal{X}}\,\,\eta \langle x, y_{j-1} \rangle + D_F(x,x_{j-1}) \\ \end{split} \label{eq:mddef} \end{equation}\]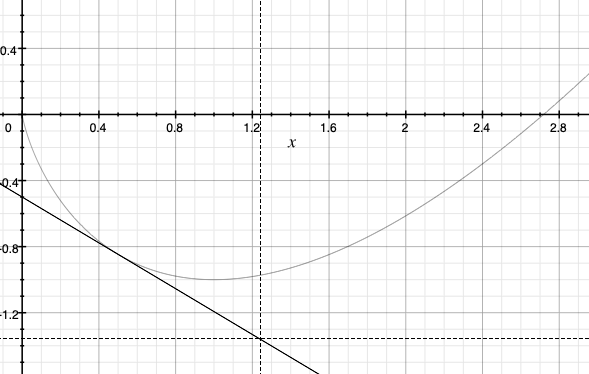 ここで
ここで
は, $F$ を \(x'\) 周りで第一階のテイラー展開したときの, $x$における剰余項である. そして簡単のため, ドメイン \(\text{dom}(F) = \{ x\in \mathbb{R}\,:\, F(x)<+\infty \}\) の内部で \(F\) が微分可能であることを前提とする. 任意の凸関数の線形近似は, 元の凸関数のグラフより下にあるため, \(D_F\) が非負であることが即座に得られる. 実例として, 凸関数と, その凸関数をある点で第一階テイラー展開したものを右図に示した.
読者は \(F\) を”非線形距離誘導関数”のようなものと考えるかもしれない. すなわち, 上記の \(D_F(x,x')\) は, \(x'\) から離れるに従い課される罰則と考えることができる. ところが \(D_F\) は距離でないことが多い. 大抵の場合, 対称性すら持たないのだ. このため, $D_F$ を距離とは呼べず, ダイバージェンスと呼ばれる. とりわけ \(D_F(x,x')\) は \(x'\) から \(x\) へのBregmanダイバージェンスと呼ばれる.
MDの更新則の定義では, 暗黙のうちに \(D_F(x,x_{j-1})\) が定義可能であることを前提としている. これには \(F\) が \(x_{j-1}\) において微分可能であることが必要とされる. このことは MD を適用するときに確認する必要がある. 我々が考える場合では, この要求も満たされている.
MDの更新則の考えは (1) 敵対者によって選ばれた直近の損失ベクトル \(y_{j-1}\) に学習者が適応することを許しつつ, (2) \(x_{j-1}\) からの \(x_j\) の逸脱を制限することで, 実質的にアルゴリズムを安定させることだ. これらのトレードオフは学習率 $\eta>0$ の選択によって決まる. (\(\eta\) を \(F\) から分離したのは, 標準的な \(F\) の選択肢が存在するだ. \(\eta\) は正真正銘ただの \(F\) のスケールパラメータに過ぎない.) とりわけ, \(\eta\) の値が小さくなればなるほど, MDはますます”データに敏感”ではなくなる. (ここでは\(y_0,\dots,y_{k-1}\)がデータを構成する) そして逆も同様であり, \(\eta\) が大きければ大きいほど, MDはますますデータに敏感になる.
なぜMirrorなのか?
\(F\) に関するいくつかの条件下では更新則\eqref{eq:mddef}は次の二段階の実装を持つ:
\[\begin{align} \tilde x_j & = (\nabla F)^{-1} ( \nabla F (x_{j-1}) - \eta y_{j-1} )\,,\label{eq:mds1}\\ x_j &= \arg\min_{x\in \mathcal{X}} D_F(x,\tilde x_j)\,.\label{eq:mds2} \end{align}\]この最初の等式が名前を説明する. \(\tilde x_j\) を計算するため, 最初に \(\nabla F: \text{dom}(\nabla F ) \to \mathbb{R}^d\) を用いて \(x_{j-1}\) を”鏡” (双対) の空間に変換する. この空間は”勾配が生息する”空間である. そして計算結果に \(-\eta y_{j-1}\) を加える. これは”勾配ステップ”と見なすことができる. (\(y_{j-1}\)は何らかの損失の勾配と解釈される) 最後に計算結果を \(\nabla F\) の逆写像を用いて元の(主)空間に戻す.
更新の第二ステップは計算結果の \(\tilde x_j\) を, ”\(F\) により誘導される空間 \(\mathbb{R}^d\) 上の幾何”を用いて, \(\mathcal{X}\) 上に”射影”することである.
“主”や”双対”空間のような複雑な学術用語の利用は多分過剰だろう. 我々の考える問題において, これらの空間はおなじみのユークリッド空間 \(\mathbb{R}^d\) に一致する. これらの空間を分けて考えることは, 無限次元空間に取り組むときに重要になるだろうが, それは置いておく.
学術用語の理解に役立つだけではなく, 上記の二段階更新は実際の計算にも役立つ. これは我々が必要な特別な場合にも当てはまる.
確率単体上での鏡像降下法
我々の問題において必要なのは
\[\begin{gather} d = \mathrm{A}\,, \mathcal{X} = \mathcal{M}_1 (A)\,, \mathcal{Y} = [-1/(1-\gamma),0]^A \end{gather}\]の場合となる.
MDを使うため, 正則関数 \(F\) と学習率を決める必要がある. 前者には
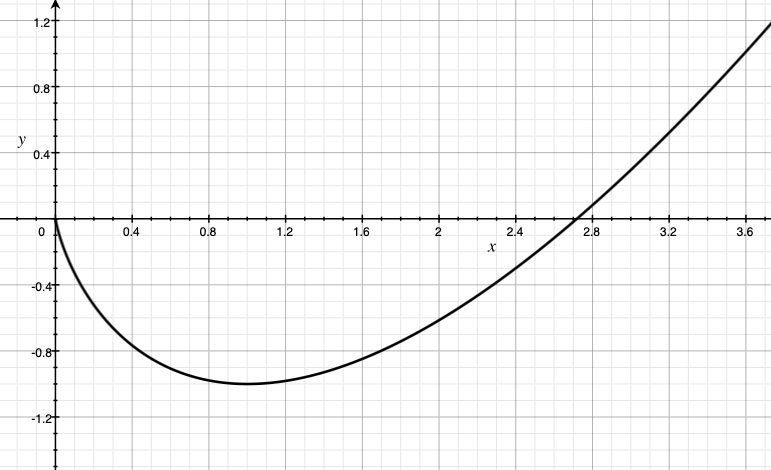
\[F(x) = \sum_i (x_i \log(x_i) - x_i)\]を用いる. これは 非正規化ネゲントロピー 関数と呼ばれる. \(F\) は \(x\in [0,\infty)^d\) において有限の値を取ることに注意しておく。 (\(\lim_{x\to 0+} x \log(x)=0\) となるので, $x_i=0$ の時には \(x_i \log(x_i)=0\) と仮定する). この象限の外では, \(F\) の値を \(+\infty\) と定める. 右図では \(x\ge 0\) における \(x\log(x)-x\) の値を示している.
\(F\) が凸であることを確認するのは難しくない: まず, \(\text{dom}(F) = [0,\infty)^d\) が凸となる. \(F\) を微分すると, 任意の \(x\in (0,\infty)^d\) に対し,
\[\nabla F(x) = \log(x)\]となる. ただし、 \(\log\) はベクトルの各要素に対して適用されている. もう一度微分すると、任意の \(x\in (0,\infty)^d\) に対し,
\[\nabla^2 F(x) = \text{diag}(1/x)\]となる。 つまり, $i$ 番目の対角要素が \(1/x_i\) の対角行列となる. 明らかにこれは正定値行列となり, \(F\) が凸であることが確認できた.
\(F\) によって誘導されるBregmanダイバージェンスは
\[\begin{align*} D_F(x,x') & = \langle \boldsymbol{1}, x \log(x) - x - x' \log(x')+x'\rangle - \langle \log(x'), x-x'\rangle \\ & = \langle \boldsymbol{1}, x \log(x/x') - x +x'\rangle \,, \end{align*}\]となる. ここで, ベクトルに関数を適用する時は要素毎に適用する (つまり, $x \log(x)$ は $i$ 番目の要素が $x_i \log(x_i)$ となるベクトル) という, “直感的”な記法を使った. $D_F$ の定義域は \([0,\infty)^d \times (0,\infty)^d\) となることに注意する. もし $x$ と $x’$ が $d-1$-確率単体の要素ならば, $D_F$ はよく知られた relative entropy, または Kullback-Leibler (KL) divergence になる.
更新式 \eqref{eq:mds1}-\eqref{eq:mds2} のようにして $x_j$ が得られた場合, これらの二段階更新が次の式で与えられることを確かめるのは難しくない:
\[\begin{align*} \tilde x_{j,i} &= x_{j,i} \exp(-\eta y_{j-1,i})\,, \qquad x_{j,i} = \frac{\tilde x_{j,i}}{ \sum_{i'} \tilde x_{j,i'}}\,, \quad i\in [d]\,. \end{align*}\]再帰式を展開して, これらの更新式は以下のように書き換えられる:
\[\begin{equation} \tilde x_{j,i} = \exp(-\eta (y_{0,i}+\dots + y_{j-1,i}))\,, \qquad x_{j,i} = \frac{\tilde x_{j,i}}{ \sum_{i'} \tilde x_{j,i'}}\,, \quad i\in [d]\,. \label{eq:mdunrolled} \end{equation}\]これに基づいて, 上記の $F$ の場合は MD の効率的な実装が可能となる. リグレットについては, 次の定理が成立する:
Theorem (ネゲントロピーを用いた確率単体上のMD): \(\mathcal{X} = \mathcal{P}_{d-1}\) かつ \(\mathcal{Y} = [0,1]^d\) とする. 学習者がMDを学習率
\[\eta = \sqrt{ \frac{2\log(d)}{k}}\]と共に用いた場合, 任意の敵対者に対し, 学習者の \(k\) ラウンド後のリグレット \(R_k\) は
\[R_k \le \sqrt{2k \log(d)}\]を満たす.
もし \(\mathcal{Y} = [a,b]^d\) ならば, MD を変換後の系列 \(\tilde y_j = (y_j-b \boldsymbol{1})/(b-a) \in [0,1]^d\) に対し適用できる. すると, 任意の $x\in \mathcal{X}$ に対し,
\[\begin{align*} R_k(x) & := \sum_{j=0}^{k-1} \langle x_j-x, y_j \rangle \\ & = \sum_{j=0}^{k-1} \langle x_j-x, (b-a)\tilde y_j+b \boldsymbol{1} \rangle \\ & = (b-a)\sum_{j=0}^{k-1} \langle x_j-x, \tilde y_j \rangle \\ & \le (b-a) \sqrt{2k \log(d)}\,. \end{align*}\]ただし, 三行目で $\langle x_j,\boldsymbol{1}\rangle = \langle x, \boldsymbol{1} \rangle = 1$ を用いた. $x\in \mathcal{X}$ に関する最大化を行い、
\[\begin{align} R_k \le (b-a) \sqrt{2k \log(d)}\,. \label{eq:mdrbscaled} \end{align}\]更新式 \eqref{eq:mdunrolled} より,
\[\begin{align*} \tilde x_{j,i} = \exp(-\eta (\tilde y_{0,i}+\dots + \tilde y_{j-1,i})) = \exp(-\eta/(b-a) (y_{0,i}+\dots + y_{j-1,i}-j b) )\,, \qquad i\in [d]\,. \end{align*}\]ここで $-jb$ 分の”シフト”は正規化によって消えることに注意する. よって, この場合の MD は
\[\begin{equation} \begin{split} \tilde x_{j,i} &= \exp(-\eta/(b-a) (y_{0,i}+\dots + y_{j-1,i}))\,, \qquad x_{j,i} = \frac{\tilde x_{j,i}}{ \sum_{i'} \tilde x_{j,i'}}\,, \quad i\in [d]\,. \label{eq:mdunrolledscaled} \end{split} \end{equation}\]この更新式は, 学習率が $1/(b-a)$ でスケールされていることを除き, 以前のものと一致する. 特にこの場合は,
\[\begin{align} \eta = \frac{1}{b-a} \sqrt{\frac{2\log(d)}{k}} \label{eq:etascaled} \end{align}\]とし, 更新式 \eqref{eq:mdunrolled} を用いればよい.
MDPにおけるプランニングに MD を適用した場合
すでに見たように, \eqref{eq:t1s} の \(T_1(s)\) は, ロスが \([-1/(1-\gamma),0]^{\mathrm{A}}\) に属する場合の確率単体上のオンライン線形最適化における \(\pi^*(s,\cdot)\) に対する $k$ ラウンドリグレットとなる. そのため、各状態毎に MD を用いることで \(T_1(s)\) を抑えられる. \eqref{eq:mdunrolled} と \eqref{eq:etascaled} から,
\[E_j(s,a) = \exp(\eta (\hat q_0(s,a) +\dots + \hat q_{j-1}(s,a)))\,, \qquad \pi_j(a|s) = \frac{E_j(s,a)}{ \sum_{a'} E_j(s,a')}\,, \quad a\in \mathcal{A}\]とすればよい。ただし
\[\eta = (1-\gamma) \sqrt{\frac{2\log(\mathrm{A})}{k}}\,.\]この更新式は Politex が使っているものと一致する. そのため, \eqref{eq:mdrbscaled} から, 全ての $s\in \mathcal{S}$ に対し,
\[\begin{align} |T_1(s)| \le \frac{1}{1-\gamma} \sqrt{2k \log(\mathrm{A})} \label{eq:t1sbound} \end{align}\]が同時に成立する. まとめると, 次の結果が得られる:
Theorem (Politex の準最適性ギャップバウンド): 特徴化 MDP $(M,\phi)$ と フルランク特徴写像 $\varphi: \mathcal{S}\times \mathcal{A} \to \mathbb{R}^d$ を考え, $K, m, H \ge 1$ とする. B2\(_{\varepsilon}\) が $(M,\phi)$ に対し成立しており, $M$ における報酬が区間 $[0,1]$ に属すると仮定する. 任意の $0\le \zeta<1$ に対し,
\[\kappa(\zeta) = \varepsilon (1 + \sqrt{d}) + \sqrt{d} \left(\frac{\gamma^H}{1 - \gamma} + \frac{1}{1 - \gamma} \sqrt{\frac{\log( d(d+1)K / \zeta)}{2m}}\right)\]を定義する。
このとき, 少なくとも確率 $1-\zeta$ 以上で, Politex が $K$ 回の更新後に出力する混合方策 $\bar \pi_K$ の準最適ギャップ $\delta$ は
\[\begin{align*} \delta \le \frac{1}{(1-\gamma)^2}\sqrt{\frac{2\log(\mathrm{A})}{K}}+\frac{2 \kappa(\zeta) }{1-\gamma} \end{align*}\]となる.
特に, 任意の $\varepsilon’>0$ に対し, $K,H,m$ を
\[\begin{align*} K & \ge \frac{32 \log(A)}{ (1-\gamma)^4 (\varepsilon')^2}\,, \\ H & \ge H_{\gamma,(1-\gamma)\varepsilon'/(8\sqrt{d})} \qquad \text{and} \\ m & \ge \frac{32 d}{(1-\gamma)^4 (\varepsilon')^2} \log( (d+1)^2 K /\zeta ) \end{align*}\]とすることで 混合方策 $\bar \pi_K$ は $\delta$-最適となる. ここで
\[\begin{align*} \delta \le \frac{2(1 + \sqrt{d})}{1-\gamma}\, \varepsilon + \varepsilon'\,. \end{align*}\]また, 全計算コストは $\text{poly}(\frac{1}{1-\gamma},d,\mathrm{A},\frac{1}{(\varepsilon’)^2},\log(1/\zeta))$ となる.
以前述べたように, G-最適設計を用いた LSPI と比べ, 近似誤差 $\varepsilon$ の増幅が $1/(1-\gamma)$ 倍分小さくなっている. その代わり、更新回数 $K$ が $\frac{1}{(1-\gamma)\varepsilon’}$ の多項式となっている. LSPI の場合, 対数的であった. もしかすると, 初期の学習率を高くすれば両者のいいとこ取りができるかもしれない.
Proof: LSPI の準最適性ギャップの 証明 で示したように, 任意の $0\le \zeta \le 1$ に対し, 少なくとも確率 $1-\zeta$ で, 任意の $0 \le k \le K-1$ に対し,
\[\begin{align*} \| q^{\pi_k} - \hat q_k \|_\infty =\| q^{\pi_k} - \Pi \Phi \hat \theta_k \|_\infty \le \| q^{\pi_k} - \Phi \hat \theta_k \|_\infty &\leq \kappa(\zeta) \end{align*}\]となる. ただし最初の不等式において \(q^{\pi_k}\) が区間 $[0, H]$ 内の値を取ることを用いた. (\(\Phi \hat \theta_k (s, a) \notin [0, H]\) の場合, $\Pi$ は \(\Phi \hat \theta_k (s, a)\) を \(q^{\pi_k} (s, a)\) に近づけるため.) 一方, この不等式が成立しているなら, \eqref{eq:polsubgapgen} と \eqref{eq:t1sbound} より,
\[\begin{align*} \delta \le \frac{1}{(1-\gamma)^2}\sqrt{\frac{2\log(\mathrm{A})}{K}}+\frac{2 \kappa(\zeta) }{1-\gamma} \,. \end{align*}\]計算の詳細は読者に任せる. \(\qquad \blacksquare\)
ノート
オンライン凸最適化, オンライン学習
オンライン線形最適化は オンライン凸/凹最適化 の一分野となる. オンライン凸/凹最適化では, 学習者は非空の凸集合 \(\mathcal{X}\subset \mathbb{R}^d\) から要素を選び, 敵対者は \(\mathcal{X}\) 上の凹関数非空集合 \(\mathcal{Y}\) から要素を選ぶ: \(\mathcal{Y} \subset \{ f: \mathcal{X} \to \mathbb{R}\,:\, f \text{ は凹} \}\). このとき, リグレットの定義は
\[\begin{align} R_k = \max_{x\in \mathcal{X}}\sum_{j=0}^{k-1} y_j(x) - y_j(x_j) \label{eq:regretdefoco1} \end{align}\]となる. ここで, 以前のように, \(x_j\in \mathcal{X}\) は \(j\) ラウンドでの学習者の選択で, \(y_j\in \mathcal{Y}\) が同じラウンドの敵対者の選択となる. 一般的な凹関数の代わりに \(\mathbb{R}^d\) のベクトル \(u_j\) を選び, $y_j$ を線型写像 \(x \mapsto \langle x, u_j \rangle\) とすると, オンライン線形最適化がオンライン凹最適化の特別な場合となる.
もちろん, \(\mathcal{Y}\) の全ての関数に $-1$ を乗じ (つまり, \(\tilde {\mathcal{Y}} = \{ - y \,:\, y\in \mathcal{Y} \}\) として), リグレットを
\[\begin{align} R_k = \max_{x\in \mathcal{X}}\sum_{j=0}^{k-1} \tilde y_j(x_j)- \tilde y_j(x) \label{eq:regretdefoco} \end{align}\]と再定義することで, 論文でよく使われる定義 (一般には凸関数が好まれる) を用いることができる. このとき, \(\tilde y_j\in \tilde {\mathcal{Y}}\) は敵対者が \(j\) ラウンド目に選ぶ”ロス関数”と考えられる.
一般的な関数の記法 (\(x\) に \(y_j\) が適用される) は非対称性を導入してしまう. 最終的には, 学習者の視点からは, \(\mathcal{Y}\) の様々な関数に対してうまく働く \(\mathcal{X}\) の要素を見つけなければならない. よって, \(\mathcal{X}\) の任意の要素は \(\mathcal{Y}\) の要素を \(y \mapsto y(x)\) を通し実数に移す関数として考えることができる. \(\mathcal{Y}\) の要素が関数であるか \(\mathcal{X}\) の要素が関数であるかはあまり意味をなさない; より重要なのは \(\mathcal{X}\) と \(\mathcal{Y}\) が相互的に繋がっている点だ. このため, オンライン学習は上記の \(y(x)\) が \(b(x,y)\) に置き換えられた問題としても考えることができる. ここで, \(b: \mathcal{X}\times \mathcal{Y} \to \mathbb{R}\) は \(\mathcal{X}\) と \(\mathcal{Y}\) の点の各ペアに利得を割り当てる. この写像が固定されているとき, \([x,y]\) を \(b(x,y)\) の代わりに用いることで, 余分な記号を省くことができる. そうすると, 線形最適化の場合の \([x,y] = \langle x,y \rangle\) とほぼ同じ記法を使うことが出来る.
切り捨てるか切り捨てないか?
解析を簡単にするため, 関数の切り捨て (値域を $[0, H]$ に制限するための射影 \(\Pi\)) を行った. これを行わなくても解析は行えるが, 準最適ギャップ (と実行時間) が僅かに増加する. この射影を取り除く利点は, \(\hat q_0 + \dots + \hat q_{j-1} = \Phi (\hat \theta_0 + \dots + \hat \theta_{j-1})\), となるので, 実用的には実行時間の大幅な削減が望めることだ.