10. Planning under $q^*$ realizability
直前の講義の教訓は効率的なプランナーはプランナーに提供される特徴量マップの不正確さからくる誤差よりも多項式的な数字で大きくなるような準最適誤差を持つ方策を誘発するという点で制限されているということであった. 私たちは次のことも見てきた. もしも私たちがこの特徴量空間の次元における誤差の増幅の多項式の誤差を許容するのであれば, 方策反復の比較的簡単な適応で計算量的に効率の良い(グローバルな)プランナーを得ることができる. これは少なくともプランナーが内在する最適実験計画問題に対する解を備えている場合が該当する. 何にせよ, このプランナーはクエリ効率が良い.
すべての内容は上記の特徴量表現による誤差がとりうるすべてのとりうる方策の行動価値関数の集合に関連しているという文脈の中で示されてきた. この講義では, 特徴量表現による誤差を最適行動価値関数$q^*$が特徴量によりどの程度うまく近似されているかにより計算でき, 一方でプランナーによるプラスの効果を維持したままにするように誤差指標を変えることができるかどうかを見ていく. 導入する方策の準最適誤差が近似誤差よりも多項式以上に大きくなるプランナーしか存在しないというマイナスの結果を暗示しているので, プランナーに提供される特徴量で最適行動価値関数が完全に表現できる場合を見ていく. 仮に使用される関数近似の手法の性質についてもっと詳しくいうと, この前提は”\(q^*\)-実現可能性”あるいは”\(q^*\) 線型実現可能性”として知られている.
\(q^*\) 実現可能性の下でのプランニング
大きな有限MDPs $(\mathcal{S},\mathcal{A},P,r)$における固定ホライゾンのオンラインプランニングを考える. いつものように, ホライゾンは$H>0$で表記され, 過去の講義と同様に固定した初期状態$s_0$でのプランニングを検討する. $0\le i \le H$ ステージ内で $s_0$ から到達可能な状態を \(\mathcal{S}_i\) と表記する. また、前と同様に, $i\ne j$の時\(\mathcal{S}_i\cap \mathcal{S}_j=\emptyset\) であり、この場合は行動価値関数は過去あるいは現在の状態に依存することを思い出そう. 各$0\le h\le H-1$について\(q^*_h:\mathcal{S}_{h} \times \mathcal{A}\to \mathbb{R}\)を$h$ ステージが実行中で$H-h$の実行が残っている最適行動価値関数とする. $\mathcal{S}_h\times \mathcal{A}$の外側では$q^*_h$の値は必要ないので, この集合を再定義することで表記を省略する.
重要な表記: ここで使用されている$q^*_h$のインデックスは過去の講義におけるインデックスとは一致しない. 過去の講義では残っているステージ数の数に基づいてインデックスを決定した方がより都合が良かったのである.
プランナーは特徴量マップ$\phi_h$を各ステージ$0\le h\le H-1$について\(\phi_h:\mathcal{S}_h \times \mathcal{A} \to \mathbb{R}^d\)となるように与えられる. この実現可能性の前提は以下のことを意味する.
\[\begin{align} \inf_{\theta\in \mathbb{R}^d} \max_{0\le h \le H-1}\|\Phi_h \theta - q^*_{h} \|_\infty = 0\,. \label{eq:qsrealizability} \end{align}\]同じベクトルのパラメータがすべてのステージで共有されることを要求することを記しておく. 後々分かるように, この仮定により結果はより強力となる. 各ステージで特徴量が異なる場合でも, 次元が$d$から$dH$に増えることを犠牲にして, パラメータベクトルが共有されることを常に前提におくことができる. プランナーのクエリ効率についてのネガティブな結果を与えるので, プランナーが特徴量マップ全体にアクセスできるようにする:プランニング処理の前あるいは処理中に特徴量マップについてのいかなる種類の計算を実行することが許されていたとしてもこのネガティブな結果は適用される.
$\delta>0$ である次のようなオンラインプランナーを $\delta$-sound for the $H$-step criterion と呼ぶ. \eqref{eq:qsrealizability} を満たす特徴量$\phi$を持つことが実現可能なMDP環境$M$の最適行動価値関数が存在する特徴量マップ$\phi = (\phi_h)_h$の組を考える. このような任意のMDP $M$と特徴量マップ$\phi$の組について, プランナーがMDP $M$において初期状態\(s_0\)から始まる$H$-ホライゾン割引なし報酬和の指標において評価される場合に$\delta$-準最適またはそれよりも良い方策をプランナーが導出する. これは近似誤差の定義が緩められた一方で$\varepsilon=0$を要求していることを除けば以前の$(\delta,\varepsilon=0)$ soundnessの指標とまさに同じであることに注意する.
下記の結果では(シミュレータから得られる)即時報酬にランダム性がありうるMDPを用いる. ランダム性のある報酬はプランナーの仕事をより難しくするために使用され, 決定的なダイナミクスのMDPを考慮することを許容する. (結果は決定的な報酬とランダム性のある遷移を持つMDPに対しても証明される.)
(余談)通常のランダムな遷移と報酬を持つMDPの定義はある意味より簡単である:そのような(有限)MDPはタプル\(M=(\mathcal{S},\mathcal{A},Q)\)で与えられる. ここでは\(Q = (Q_a(s))_{s,a}\)は状態報酬対に対する分布の集合である. 特にすべての状態行動対$(s,a)$について, \(Q_a(s)\in \mathcal{M}_1(\mathcal{S}\times\mathbb{R})\)とする. \((S',R)\sim Q_a(s)\)(すなわち$(S’,R)$はランダムに\(Q_a(s)\)から取得される.)とすると, $S’$の分布として$P_a(s)$, $R$の期待値として$r_a(s)$という形で修復できる. 報酬にランダム性があっても良いことは標準確率空間の表記に変化を与えることを強制する, というのも現在の履歴は各タイムステップ$t=0,1,\dots$で生じた報酬$R_0,R_1,\dots$を含んでいるからである. 適切に式変形することで, それにもかかわらず\(\mathbb{P}_\mu^\pi\)と対応する期待作用素\(\mathbb{E}_\mu^\pi\)を同様に導入できる. 状態$s$における方策$\pi$の価値の自然な定義は, たとえば, 割引付き設定では\(v^\pi(s) = \mathbb{E}_s^\pi[ \sum_{t=0}^\infty \gamma^t R_t]\)となる. ところが, 任意の$t\ge 0$ で\(\mathbb{E}_\mu^\pi[R_t]=\mathbb{E}_\mu^\pi[r_{A_t}(S_t)]\)となるのを確認するのは容易であり, したがって, これまでに得られた理論的結果において何も変化しない.
実数$a,b$において $a\wedge b = \min(a,b)$としよう. この講義の主な結果は以下の通りである:
Theorem (最悪ケースのクエリコストは$q^*$-実現可能性の下で指数関数的): 任意の十分に大きい$d,H$と$H$ホライゾンのプランニング問題において$9/128$-soundである任意のプランナー$\mathcal{P}$について, 次のようなトリプレット$(M,s_0,\phi)$が存在する. ここでは$M$は$[0,1]$の範囲にある値を取るランダム性のある報酬を持ち遷移は決定的であり, $s_0$をMDPの状態にもつ. $\phi$は$d$次元の特徴量マップで\eqref{eq:qsrealizability}を最適行動価値関数\(q^* = (q^*_h)_{0\le h \le H-1}\)について満たし, プランナー$\mathcal{P}$が使用するクエリ$q$の期待値は$(M,s_0,\phi)$と相互接続されている時, 以下の数値を満たす. \(q = e^{\Omega(d\wedge H )}\)
tail behaviorについて制御されないランダム性のある報酬では任意のプランナーの仕事を好きなだけ難しくできることに注意してほしい. (例:分散に制限がない場合) したがって, この結果を得るために構築されたMDPにおいて, 報酬が確率的であっても固定された区間に収まっていることが重要である. この区間の特定の選択は重要ではないことに着目する. もしもある空間で難しい例があるなら, その例は移動やスケーリングおよびその変換を説明するための追加の次元を特徴量マップに加えることを犠牲にして別のものに置き換えることができる. 似たような主張が$\delta = 9/128$にも適用される. (これはそういったことを関係なしに報酬の範囲をスケールする必要がある.)
証明のメインとなる考え
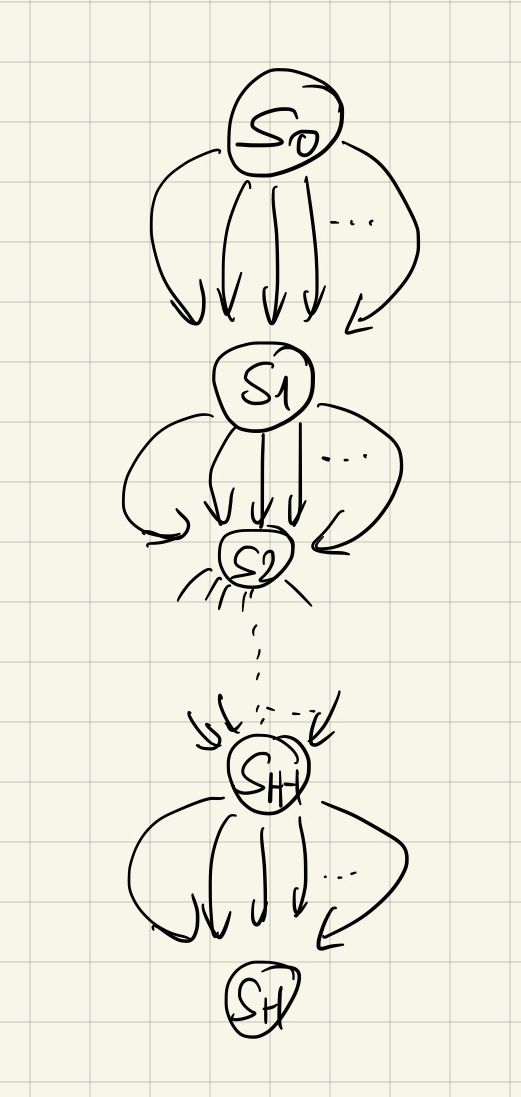
証明全体を与えるよりも, その背後にあるメインとなる考えを説明しよう. 高レベルでは, この証明は小規模な行動集合の場合と大規模な行動集合の場合の両方のlower boundの証明のアイデアを用いる. そういうわけで, $d$に関して指数関数的な行動集合について検討する. 特に, 行動集合が$k=e^{\Theta(d)}$ の要素を持つ場合を検討する.
実現可能性を保つために, 大規模だが単純なダイナミクス(直前の講義におけるlower boundにおける場合と同様)を持つ行動集合は望んだ形のlower boundを導くことはできないことに注目してほしい. 特に, もしもダイナミクスが単純(例 $\mathcal{S}_i={s_i}$, 右の図を参照)であれば, $s_0$で取られる最適行動は後のステージで何の行動がとられるかに依存せず, そのステージで得られる報酬を最大化するだけで効率的に最適行動を見つけることができる. これは私たちの実現可能性の前提によると効率的に実施でき, ランダム性のある報酬がある場合でさえも同様である. 行動は少数だがより複雑なダイナミクスを持つ場合が問題としてまだ残っている. ここで提供される構成(木構造のダイナミクスに基づいており, 木の中では即時報酬は$0$になる)では, 下で明らかにするように, 実現可能性を明らかに満たさない.
なんにせよ, “chain dynamics”は機能しないので, 次の最も単純なアプローチは木を持つが, 各ノードで指数関数的に大きな行動集合をもつ場合である. このケースでは非常に多くの状態を持つ(ステージ$h$ごとに$e^{\Theta(dh)}$の状態を持つ)ので, 次の疑問はどのように実現可能性を保障するかということにある. ここでは二つの問題がある:一つ目は各ステージで次元を$d$に固定し続けることができる必要があること, 二つ目は各ステージで各状態について最適な行動がどれなのかを制御する方法を持つ必要があることである. 実際に, 実現可能性はすべての$0\le h \le H-1$ および $(s,a)\in \mathcal{S}_h \times \mathcal{A}$について以下の式を満たす必要があることを意味する.
\[\begin{align} q_{h}^*(s,a) = r_a(s)+v_{h+1}^*(sa) \label{eq:cons} \end{align}\]ここでは$sa$は状態$s$で行動$a$を取ることで到達できる状態を意味する.(木の中では, すべてのノードあるいは状態はその状態に到達する際の行動系列によってユニークにインデックスされる.) 今や, すべての$h$について$v_{h}^*$の定義では, \(v_{h}^*(s) = \max_{a\in \mathcal{A}} q_{h}^*(s,a)\)となり, これは最大化させる行動の正体を知る必要性を要求する. さらには, ベルマン最適作用素に対する解はユニークなので, もしも\eqref{eq:cons}が何らかの特徴量とパラメータのベクトルですべての状態行動ペアについて\(q_h(s,a) = \langle \phi_h(s,a), \theta^* \rangle\)を満たすこと保障すれば, \(q_h = q^*_h\)がすべての\(h\ge 0\)について成立することになり, すなわちその特徴量で\(q^*\)は実現可能であることを意味する.
これらの問題全てを解決する簡潔なアプローチは固定した行動 $a^*\in \mathcal{A}$ をすべてのステージで最適な行動とし, 過去の講義で扱ったJL特徴量を併用することである.(もちろんこの行動の正体はプランナーには隠されている). とりわけ過去の講義にあったJL feature-matrix lemmaは$k$ $d$次元の単位ベクトル$(u_a)_{a\in \mathcal{A}}$をもち, このベクトルは$a\ne a’$で以下を満たす.
\[\begin{align*} \vert \langle u_a, u_a' \rangle \vert \le \frac{1}{4}\,. \end{align*}\]これらのベクトルを固定する. $a^*$がすべての状態$s$で最適でなければならないことは以下の式と等価である.
\[\begin{align} q_h^*(s,a)\le q_h^*(s,a^*) (=v_h^*(s)), \qquad 0\le h \le H-1, s\in \mathcal{S}_h, a\in \mathcal{A}\,. \label{eq:aopt} \end{align}\]以前の証明では私たちは\(\phi_h(s,a) = u_a\) と \(\theta^* = u_{a^*}\) を使用していた. これはまだ機能するのだろうか? 残念ながら機能しない. 一つ目の観測はこのことからすべての$h$, $s$, $a$について以下の式が成立することである.
\[\begin{align*} q_{h}^*(s,a) = \langle u_{a^*}, u_a \rangle\,. \end{align*}\]したがって, ほとんどすべての行動 $a$ について, JLの補題の性質から$\vert{q^*}_h(s,a)\vert$は$1/4$に近くなることが予期される.
今や, この選択の下ではJLの補題から ${v^*}_h(s)=1$がすべての状態とすべてのステージ$0\le h \le H-1$について成立する. これは私たちが上の方で簡単なchain-dynamicsの形で見た問題と本質的に同じ問題を作っている.
とりわけ, \eqref{eq:cons}から \(q_h^*(s,a) = r_a(s)+1\)が得られる. 従い, $r_a(s)$ は$-3/4$ あるいは $-5/4$ のどちらかに近づくことを予期される.(なぜなら \(|q_h^*(s,a)|\) は$1/4$に近づくので) 即時報酬が $[0,1]$の範囲に収まってほしい点を置いておくと, もし報酬のノイズが大きくなければ, \(\theta^*\), したがって $a^*$の正体はわずかなクエリで獲得できる. すなわちシグナルノイズ比が良すぎてlower boundを導くのに適していない.
同様の問題は最後のタイムステップ $H$ でも生じる. すなわちここでは任意の状態$s’$について$v_H^*(s’)=0$が成立する. ゆえに任意の$(s,a)$の組について式(4)が成立する. \(\begin{align} q^*_{H-1}(s,a)=r_a(s) \label{eq:laststage} \end{align}\)
\(q^*_{H-1}(s,a)\)を例えば $e^{-\Theta(H)}$ のように小さく選ばない限りは, プランナーは私たちが望んだバウンドよりも小さいクエリ数でプランニングを成功する.
これは何らかのスケーリング因子で特徴量のスケーリングを導入する動機を与える.(パラメータベクトルはステージ間で共有されていることを思い出そう) 最大限一般化する場合, \((s,a)\in \mathcal{S}_h\times \mathcal{A}\)の特徴ベクトルのスケール因子が\((s,a)\)自体に依存しても良い.(なぜならステージ間で状態は共有されていないのでスケーリングはこの選択にのみ依存することができるからである) \((3/2)^{-h+1}\sigma_{sa}\)を\((s,a)\)と共に使用する意図を持つスケーリング因子としよう. ここでは$\sigma_{sa}$が定数範囲に収まり続けるようにする(したがって意図した通りのステージのインデックスを用いたスケーリングになる)一方で\(\phi_h(s,a) =(3/2)^{-h+1} \sigma_{sa} u_a\)を使用することを狙う.
今や行動の数が多い場合の必要性を説明できる. ベルマン最適方程式\eqref{eq:cons}より, 任意の準最適行動$a$について以下の式が成立する.
\[r_{a^*}(s)-r_a(s) =q_h^*(s,a^*)-q_h^*(s,a) \approx (3/2)^{-h} \langle u_{a^*}-u_a,u_{a^*} \rangle \ge (3/2)^{-h} (3/4),\]ここでは\(\approx\)は\(\sigma_{sa}\approx\sigma_{sa^*}\approx \text{const}\)の意味で使用する. このことから初期状態\(s_0\)の付近では報酬のギャップは定数オーダーになるとわかる. 特にもしも状態ごとに僅かな行動しか存在しないのであれば, プランナーは他よりもとても大きい報酬を持つ行動を見つけることで最適行動を特定できる. 行動の数が多いケースを選ぶことで, プランナーは”藁針問題”の状況に直面する. これでは(ノイズのない)完全な信号があったとしてもうまく機能しなくなってしまう.
次のアイデアは「賢い」プランナーに最後のステージで用いた行動だけで実験させる方法である。ここから、シグナルノイズ比はとても悪くなり、これ(\(q^*\) 実現可能性の下でのプランニング?)をなんとか達成しようとするとより賢いプランナーでも膨大な数のクエリが必要となる。これ(?)を強いる簡単な方法は、木を遷移する時に非最適な行動を選択した場合の報酬をすべてゼロにする方法である。ただし、ステージ $h=H-1$ では以前のプランと整合するように報酬はランダムに選択するが、シグナルノイズ比は悪くなる(?)。
木の状態遷移は既知であり、最適な行動を選択しない限り報酬はゼロであるため(最適な行動は指数的に増加する行動のうちのただ一つであるためそれを発見するのは難しい)、プランナーはランダムに行動して最適行動を見つけるような干し草の中から針を見つける問題を解くか、最後のステージで行動を試す必要がある。ただし、報酬が等しくゼロであることよりも全て同じ値であることが問題となる。
一貫性が得られること(一貫性って何?)と状態 $s_0$ における最適行動が同じ状態における准最適な行動に比べて高い価値を持つかどうかについてはまだ確認できていない。ここで、一貫性についていくつかの問題に直面する。即時報酬が $[0,1]$ であることを仮定しているため、全ての行動価値は非負となる。そこで、ステージによって行動価値の値をスケールすることができるように特徴ベクトルにバイアス項 $c_h$ を導入する。つまり、ステージ $h$ での特徴量を
\[\begin{align*} \phi_h(s,a) = ( c_h, (3/2)^{-h+1} \sigma_{sa} u_a^\top )^\top\,. \end{align*}\]とし、次のベクトルを用いることを提案する
\[\begin{align*} \theta^* = \frac{1}{3} (1, u_{a^*}^\top)^\top \,. \end{align*}\]ただし、 \(q_h(s,a):=\langle \phi_h(s,a), \theta^* \rangle = \frac{1}{3}\{ c_h + \frac{3}{2}^{-h+1}\sigma_{sa} u_{a^*}^Tu_a \}\) のときに (1) \eqref{eq:aopt} と \eqref{eq:cons} を満たし、 (2) 状態 $s_0$ において \(a^*\) が非最適な行動との価値の差を大きく保ち、 (3) 最後のステージでの報酬 (\eqref{eq:laststage}) が $[0,1]$ に収まりつつ \(e^{-\Theta(H)}\) のサイズである、という3つの条件を満たすことはまだ確認できていない。
ここで、しばらくの間 \(a^*\) が全ての状態で最適、つまり \eqref{eq:aopt} が成立すると仮定する。すると、 \(a^*\) は 状態 $sa$ でも最適であり、 \(q^*_h=q_h\) のもとでは全ての \(a\ne a^*\) は以下と等しい。 \(\begin{align*} q_h(s,a) = q_{h+1}(sa,a^*) \end{align*}\) ここで \(a\ne a^*\) なので $r_a(s)=0$ という仮定を用いた。定義に代入すると($\sigma_{sa,a^*}$ の定義どこ?誤訳かも)以下を得る。
\[\begin{align} \sigma_{sa,a^*} = \left(\frac{3}{2}\right)^h \left(c_h-c_{h+1}\right) + \frac{3}{2} \sigma_{sa} \langle u_a,u_{a^*} \rangle\,. \label{eq:sigmarec} \end{align}\]\(C_{H-1} = \frac{1}{2}\left(\frac32\right)^{-H}\) (つまり、バイアス項 $c_h$ は単調減少する等比級数である) として \((c_h)_{0\le h\le H-1}\) を下記を満たすように定義する。
\[\begin{align*} \left(\frac{3}{2}\right)^h \left(c_h-c_{h+1}\right) =\frac{5}{8}\,. \end{align*}\]すると、この式は2つのことを意味する。つまり、\eqref{eq:sigmarec} は次のように簡易的に表現できる。
\[\begin{align} \sigma_{sa,a^*} = \frac{5}{8} + \frac{3}{2} \sigma_{sa} \langle u_a,u_{a^*} \rangle\,, \label{eq:sigmarec2} \end{align}\]また、最後のステージの報酬について、 \eqref{eq:laststage} から以下を得る。
\[\begin{align*} r_a(s) = \frac{1}{3} \left(\frac32\right)^{-H} \left( \frac{1}{2} + \sigma_{sa} \frac32 \langle u_a,u_{a^*}\rangle\right)\,. \end{align*}\]\(a\ne a^*\), \(\vert \langle u_a,u_{a^*}\rangle \vert \le 1/4\) であることから、 $\sigma_{sa}\in [-4/3,4/3]$ のとき明らかに \(r_a(s)\in [0,(3/2)^{-H}/3]\) であり、また \(r_{a^*}(s)\in [0,1]\) である。
以上から、 \eqref{eq:cons} を満たすために、次のように木の中で「再帰的に? (downward recursion)」 $\sigma_{sa}$ を定める:木の中の任意の $s$ と行動 $a,a^\prime$ について \(\begin{align} \sigma_{sa,a'} = \frac{5}{8} + \frac{3}{2} \sigma_{sa} \langle u_a,u_{a'} \rangle\,. \label{eq:sigmarec3} \end{align}\)
これは \eqref{eq:sigmarec2} と一致することに注意したい。
次の問題は $\sigma_{sa}$ が固定された区間の中にあることを示すことである。実際、上記定義ではこれは成立しない。特に、 $a=a’$ のとき右辺は \(5/8+3/2 \sigma_{sa} \ge 3/2 \sigma_{sa}\) となり、スケール係数が $3/2$ を基底として指数的に大きくなる。しかし、$a\ne a’$ の場合は、 \(\sigma_{sa}\in [1/4,1]\) (初期状態 \(s_0\) で全ての行動 $a$ について \(\sigma_{s_0,a}=1\) のときにこれは成立する)とすると、
\[\frac{1}{4} = \frac{5}{8} - \frac{3}{8} \le \frac{5}{8} + \frac{3}{2} \sigma_{sa} \langle u_a,u_{a'} \rangle \le \frac{5}{8} + \frac{3}{8} \le 1\,,\]であり、したがって \(\sigma_{sa,a'}\in [1/4,1]\) は成立する。
そこで、$a=a’$ のときに \eqref{eq:sigmarec3} を必要としないようにできないか考える。これはダイナミクスを変更することで達成できる。つまり、新たに exit lane と呼ぶ特別な状態集合 ${e_1,\dots,e_H}$ を導入する。エージェントはこのレーンに一度入ると、リターンとエピソード終端までの全ての報酬はゼロとなる。特に、状態 $e_h$ における全ての行動は状態 $e_{h+1}$ に導き、 exit lane における特徴ベクトルは次のように全ての状態においてゼロベクトルとする。
\[\phi_h(e_h,a) = \boldsymbol{0}\,.\]このように、パラメータベクトルの選択に関わらず、これらの状態においてベルマン最適方程式が成立すること、また最適価値がゼロになることを保証する。
Exit lane は行動を繰り返す場合において \eqref{eq:sigmarec3} を使う必要がないようにするために導入した。特に、ある $h\ge 1$ における任意の \(s\in \mathcal{S}_h\)、例えば \(s=(a_1,\dots,a_h)\) (つまり、 $s$ はこれらの行動により得られる)を考えると、\(a\in \{a_1,\dots,a_h\}\) のときに次の状態が $e_{h+1}$ になるとする(?)。$e_{h+1}$ の最適価値はゼロなので、即時報酬は導入せずに
\[\phi_h(s,a)=\boldsymbol{0}\,,\]のように設定して、行動の繰り返し(ToDo: つまり全ての行動は同じと仮定している?)における価値をゼロにする。次に難しい点が、exit lane を用いることが全ての状態において \(a^*\) を最適にするという計画を台無しにしてしまうということである。確かに、 \(a^*\) は \(s_0\) から木構造の葉までの一つのパスにおいて繰り返し適用することができるが、新しく導入したルールによって $a^*$ の価値がゼロになる。したがって、行動が \(a^*\) の場合においてはこのルールを修正する必要がある。
明らかに、非最適な行動、または \(a^*\) が繰り返されることは $\sigma_{sa}$ の再帰的な定義にとっては問題となる。そこで、 \(a^*\) も強制的に exit lane を使うように仮定する方が良い。したがって、 \(h\ge 0\) のときに \(s\in \mathcal{S}_h\) で \(a^*\) が使われた場合、次の状態を \(e_{h+1}\) とする。一方、 \(\sigma_{sa^*}\) はゼロとせずに、再帰的な定義を保ち、 \(q_h(s,a^*) = \langle \phi_h(s,a^*), \theta^* \rangle\) となるような即時報酬を導入する。この報酬が \([0,1]\) であることを確認することは難しくない(?)。ここで、 \(s = (a_1,\dots,a_h)\) の場合定義から \(a^*\not\in \{a_1,\dots,a_h\}\) であることに注意する(ToDo: 同じ行動を選ぶのではなかったっけ?)。これによりMDPsの構造を記述することができた。
$s_0$ において行動の差が大きいことは JL 特徴ベクトルの選び方に依存する。
\(a^*\) が任意の状態において最適行動かどうかはまだ分かっていない。これは、 \(a'\ne a^*\) のときに \(q_{h+1}(sa,a^*)-q_{h+1}(sa,a')\ge 0\) であるかを確認すればよい。 \(a'\) が繰り返し行動の場合これは簡単である。\(a'\) が繰り返し行動ではない場合、以下を得る。
\[q_{h+1}(sa,a^*)-q_{h+1}(sa,a') = \frac{1}{3}\left(\frac{3}{2}\right)^{-h} \left[ \sigma_{sa,a^*}-\sigma_{sa,a'}\langle u_{a'},u_{a^*}\rangle \right] \ge \frac{1}{3}\left(\frac{3}{2}\right)^{-h} \left[ \frac{1}{4}-\frac{1}{4} \right] = 0\]ただし、 \(\sigma_{sa,a^*}\ge 1/4\) と \(1/4\le \sigma_{sa,a'}\le 1\) をもちい、したがって \((u_a)_a\) の選択と \(a\ne a'\) によって \(\sigma_{sa,a'}\langle u_{a'},u_{a^*}\rangle\ge -\frac{1}{4}\) となる。
ここで、 \(M_{a^*}\) を最適行動を \(a^*\) とするときに、上記のように構築された MDP とする(特徴マップはもちろんこれらのMDPsで共有する)。正式に証明するためには、クエリーをたくさん使わないプランナーはこれらのMDPを区別できないことを論証する必要がある。直感的には、そのようなプランナーはMDPは異なるものの高確率で同じ観測結果を受け取るからである。そのため、これらのプランナーはせいぜいランダムに行動を選択するしかなく(干し草針問題)、MDP $M_a$ では行動 $a$ のみで高い価値を得られるので准最適な価値を生成できる方策を見つけることはできない。
多くの行動での計算
ここまでの構成では、行動の数は行動次元に比例して指数的に増加することが許されている。上の証明では、もし次の(簡易的に $h$ への依存を省略して示す)最適化問題
\[\begin{align*} \arg\max_{a\in \mathcal{A}} \langle \phi(s,a), \theta \rangle \end{align*}\]を解く際に、$\theta\in \mathbb{R}^d$ と $s\in \mathcal{S}$ に依存しない計算効率が良いJL特徴ベクトルを選択できると示せる場合に、プランニングにおけるクエリと計算複雑度を分離できることを示している。そのようなソルバーが存在するかどうかは特徴マップの選び方に依存し、それ自体が興味深い質問である。ひとつのアプローチはこの問題を $V_s \subset \mathbb{R}^d$ を特徴ベクトル \(\{ \phi(s,a) \}_{a\in \mathcal{A}}\) の凸包 にしたときに以下のように問題を書き換えることである。
\[\begin{align} \arg\max_{v\in V_s} \langle v, \theta \rangle \label{eq:linopt} \end{align}\]この問題が効率的な解を持ち、任意の $V_s$ の極点が与えられたときに $\phi(s,a)=v$ となるような行動 $a\in \mathcal{A}$ を効率的に見つけられる(これは特徴マップを「反転」することに相当する)ならば、最初の問題も効率的に解くことができる。
\eqref{eq:linopt} は凸集合 $V_s$ における線形最適問題であり、この問題を解く効率的なソルバーがあるかどうかはコンピュータサイエンスの根幹であることに注意する。一般的な教訓としては、$V_s$ が定義に使われた記述以外の何らかの「便利な」記述を持つとき、答えは「イエス」であると期待できるということである。特徴量マップを反転させる2つ目の問題は「分解問題」として知られていて、この問題についても同様の結論を得る。
ノート
- 上記の議論を修正し、割引付きの設定においても対応することはできる。以下に引用する論文にその方法が示されている。
- 有限ホライゾンの設定では、上界について宿題2で扱った最小二乗価値 $G$-最適反復アルゴリズムの設計を用いることができる。このアプローチを用いると、
のオーダーのクエリ効率(計算コストも似たオーダー)の $\delta$-sound なプランナーを得られる。下界と上界の指数を見ると、上界の指数は \(\Theta(H \log_2(d))\) で下界の指数は \(O(H\wedge d)\) である。このように、両者の間には $H\ll d$ では対数的なギャップが有り、 \(H \gg d\) 、つまりホライゾンが長い場合はギャップは無制限となる。特に、固定次元でホライゾンが長い計画問題の場合、 LSVI-G アルゴリズムはステージ毎に最適行動価値関数を計算しているので最適とはいえないようである。LSVI-Gの上界はタイトであり、本講義における下界も正しいと推測される?。これは、特徴次元が一定であるホライゾンが長い計画問題において、LSVI-Gよりもはるかに良い性能を発揮する代替アルゴリズムが存在することを示唆する。明らかに、本講義で用いた特定の構成では、例えば\(s_0\)で全ての行動を試すプランナーは最適な行動を見つけ、このプランナーのコストは水平線に依存しない。
したがって、少なくともこの場合、下界は代替アルゴリズムで対応可能である。 この問題は純粋に理論的な興味しかないと読者は思うかもしれない。しかし、長いホライゾンの計画は本当に重要な実用的問題であることに注意されたい。多くのアプリケーションでは、数百万とまではいかなくても、数千のステップが必要であり、一方、特徴空間の次元はそれほど大きくなくてもよいかもしれない。LSVI-Gよりも優れたアルゴリズムが存在するかどうかは、アプリケーションに大きな影響を与える可能性のある、魅力的な未解決問題のままである。
- 無限割引なし問題と \(v^*\) 実現可能性について、 \(\Theta(d)\) の行動と $d$ 次元特徴量を用いて、固定の非最適ギャップを保証するためには任意の状態に対して \(\Omega(2^d/d)\) のクエリが必要であることを示す簡単な例がある。これはグリッド上の最適経路問題をベースにしている。ここで、障害は単純な代数的なもので、遷移にも報酬にもノイズがない。
参考文献
本講義は下記の論文(arXiv。ALTで発表される)をもとにしている。
- Weisz, Gellert, Philip Amortila, and Csaba Szepesvári. 2020. “Exponential Lower Bounds for Planning in MDPs With Linearly-Realizable Optimal Action-Value Functions.”,
The second lower for the undiscounted setting mentioned in the notes is from
- Weisz, Gellert, Philip Amortila, Barnabás Janzer, Yasin Abbasi-Yadkori, Nan Jiang, and Csaba Szepesvári. 2021. “On Query-Efficient Planning in MDPs under Linear Realizability of the Optimal State-Value Function.”
available on arXiv.
上記線形最適問題に関する非常に優れた参考書は以下。
- Grotschel, Martin, László Lovász, and Alexander Schrijver. 1993. Geometric Algorithms and Combinatorial Optimization. Vol. 2. Algorithms and Combinatorics. Berlin, Heidelberg: Springer Berlin Heidelberg.